Machine-learning-ex1

序

　　这个系列是关于coursera上吴恩达的machine learning课程的文章。主要内容将包括每个week的编程练习作业，也可能会有一些笔记，知识的整理等，记录下自己学习这个课程的一些心得和体会。本文的主要内容是week 2的编程练习。

为什么要写这个系列？

　　恩，可能只是一时冲动而已吧。首先，通过前面写的关于csapp系列文章，笔者觉得还是应该养成一个写博客的习惯吧。虽说写博客花的时间真的挺多的(前面的那几篇文章基本上至少半天，多的话要写一天甚至更多)，但很明显还是能感觉得到写完博客之后对于知识的理解还是更加清楚了一些，基本上重新看一遍能够回想起当时做的时候的思路历程。并且尽管这个教程算是很有名了，但是网上的一些资料质量还是参差不齐，不少都有着各种各样的问题。因此，笔者决定自己来写这个系列，一是为了加深理解，便于日后重新回顾，二是希望能够给恰好点开了这篇文章的同学一点点帮助。当然，由于笔者目前水平有限，且笔者也是第一次接触机器学习，难免会出现各种各样小问题，如果你发现了一些问题，也欢迎与我联系(点击右下角的小图标即可，可能要稍微等一会)。

Octave 的安装问题

　　笔者的系统为 archlinux: 4.20.0
　　在安装过程中，出现了一些找不到共享库的情况，类似于这样的错误：

error while loading shared libraries: libxxx.so

　　遇到这种错误的时候，其实安装对应的库就行了，比如libreadline.so的库名称为readline。直接用对应的系统的下载命令即可。(笔者用的是 yay xxx命令)。不过，安装的时候记得看清楚提示，笔者就是因为没注意提示然后导致libreadline.so库丢了，然后开机都没办法，最后还是用U盘上的系统把这个库拷贝过来才解决的。

任务正文

实验如何提交

　　首先，在octave下，进入ex1文件夹中(octave可以使用linux系统的ls, cd命令)，然后直接输入submit即可，顺利的话很快就可以看到结果。做完所有任务的话看到的信息应该是这样:
message

　　不过，笔者在octave中，submit后就直接卡住了，应该是网络的问题，被墙了。笔者采用的解决办法是使用proxychains代理运行octave，然后submit就成功了。不同系统的话解决办法不一定相同，但总之注意好代理应该就可以了。下载的时候也是，笔者是采用proxychains + curl命令直接下载文件的。

one feature

　　这个实验我们必须完成的函数仅为一个特征的情况，难度较小。one feature下我们需要填写的文件有：

warmUpExercise.m 用于练习submit
plotData.m 用于data的可视化
computeCost.m 计算代价函数J(theta)
gradientDescent.m 实现梯度下降算法

　　主要是为了测试一下submit能否正常运行。其中，第一个文件答案仅一行(注意不要漏了分号)。

1	A = eye(5);

　　第二个文件答案只要照着pdf打即可。

1
2
3

plot(x, y, 'rx', 'MarkerSize', 10);
ylabel('Profit in $10,100s');
xlabel('Population of City in 10,000s');

　　注意，其中plot的用法(可以输入help plot查看)。’r’表示红色，同理可以换成’b’,’g’等。’x’表示用X来展示每个数据，同理可以换成’o’，表示用圆圈来展示等。最后’markerSize’表示每个标记的大小为10，可以修改这个数字自己看一下效果，也可以输入’LineWidth’，’color’等，具体效果可以自行尝试。

代价函数的计算

　　这里代价函数计算单特征和多特征的写法是一样的，因此放在一起写。请务必保证每一步都可以理解清楚，建议画图加深理解。
　　首先，我们观察h_θ(x)的计算公式：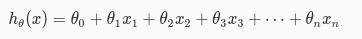
h(x)
　　用X表示我们的m * (n+1)的数据集，其中，m表示example数量，n表示特征数量，则X是一个m * (n+1)的矩阵。
　　用theta表示我们当前的变量theta，时刻记住，theta是一个n维的向量(m * 1)，n与特征数相对应。因此，用向量化的思想，h(x)即可以表示为X * theta，注意矩阵乘法是不可交换的。相乘之后我们得到一个m维的向量，即m个example各自对应的预测值，再减去实际值y(y同样是一个m维的向量)，即得到我们误差向量c。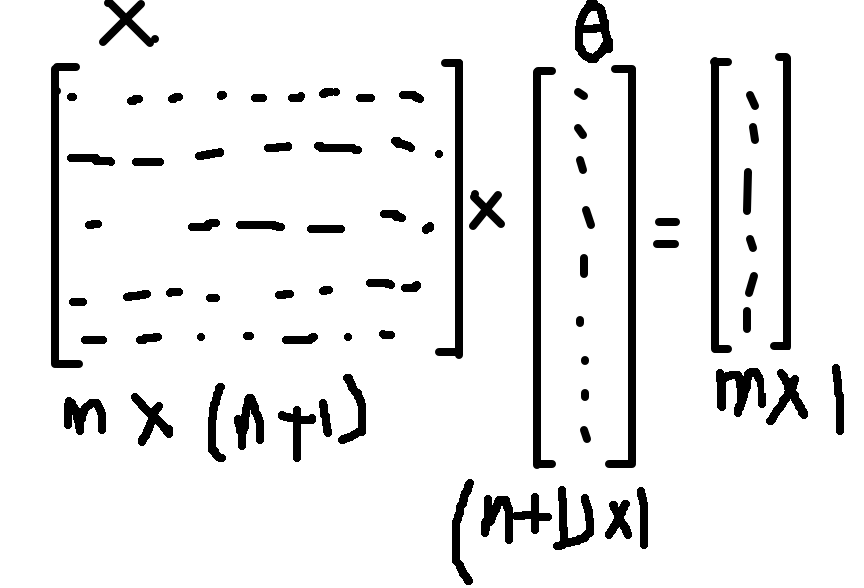
h(x)
　　而最后我们要的应该是每一个误差的平方再除以2m，可以用c’和c相乘即可。
　　最后的答案为(c’ * c 也可以写成 sum (c .* c)，没有区别)。

c = X * theta - y;
J = c’ * c / (2 * m);

梯度下降算法的实现

　　梯度下降算法多特征理解起来可能还是有一点难，强烈建议画图，并且通过图好好理解。
　　首先，还是先来看一下公式。对第j个theta，我们要进行如下的更新，而且所有的theta应该同时更新。注意，具体计算的时候，我们把theta看成是一个n + 1维的向量。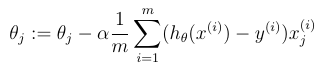
h(x)
　　即我们可以看成：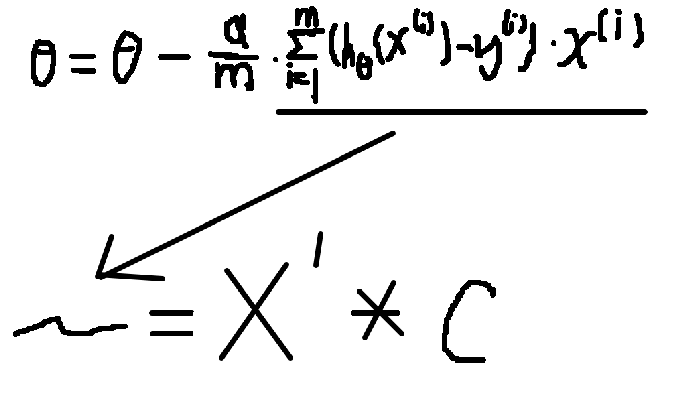
h(x)
　　这个时候别忘了，在上面的公式中，我们的变量是theta，也就是说，i可以理解成是一个常数。右边的x⁽ⁱ⁾应该也是和theta对应的一个m维的向量，而X即我们的数据集。而i是常数，因此，h_θ(x⁽ⁱ⁾) - y⁽ⁱ⁾也是一个常数。h_θ(x)-y应该是一个m维的向量。
　　用c表示该向量，则X’ * c 即可以表示上面的公式中sigma右边试子的值。
　　因此，最后的答案为:

c = X * theta - y;
theta = theta - X’ * c * alpha / m;

　　两个文件写完之后，我们可以运行ex1，查看我们的结果和预期的结果是否相同，最后成功的话应该可以看到一条直线基本上能拟合我们的数据，说明应该是成功了。这个时候我们就可以submit上去了。

multiple features

　　这个练习后面又有一个选择性的练习，即多特征下的梯度下降，整体思路其实很相似。
　　对于多个特征的数据，很多情况下，我们需要先将其标准化，以减少迭代次数。这里，我们使用mean和std函数帮助我们的计算。

mu = mean(X);
sigma = std(X);
X_norm = (X - mu) ./ sigma;

　　其中，X为我们的数据集，而X中的每一列即表示我们某一个特征的所有数据。mean(X)求出矩阵X每一列的平均值，存储在向量mu中。std(X)求出每一列的标准差，存储在向量sigma中。最后对X中的每一列，每一行的数字减去该列的平均值，再除以方差即完成标准化的步骤。
　　然后，我们需要完成computeCostMulti.m 和 gradientDescentMulti.m 文件，实现多特征的梯度下降算法，具体写法上面已经有写，这里不再赘述。倘若没有问题，输入ex1_multi后，我们应该可以看到以下的输出：
h(x)
　　然后，我们需要修改ex1_multi中的值，有h(x)的计算公式，我们很容易得到price应该是：

price = [1,1650,3] theta;

　　好了，这个时候我们倘若运行，会发现预测得到的price极其大，而我们通过看几个数据，发现price应该是在30w上下的，是我们梯度下降做错了吗？其实并不是，这里有一个坑。我们前面用到了特征的归一化，而对于我们要预测的值，我们并没有进行处理，这个时候得到的答案显然就是错误的。正确的答案应该是：

price = [1,([1650,3] - mu) ./ sigma] * theta;

　　注意，计算mu和sigma的时候我们还没有的x₀还没有加上去。因此预测值向量应该是[1,([1650,3]-mu) ./ sigma]。最后得到的答案是29w多一点。
　　接着，文档中又给出了一个选择alpha的测试，有兴趣的话可以改一下ex1_multi中的alpha变量，看一下收敛需要的迭代次数的变化。
　　最后，是一个标准方程的测试，我们将公式直接输入进去即可。具体原理暂时不懂，等学完线性代数再去理解吧。

theta = pinv(X’ * X) * X’ * y;

最后

　　到这里，整个实验的所有题目就结束了，然而这样真的就全部完了吗？笔者还发现了一个小细节，不知道是不是作者故意留下来的。如果你写法和我一样的话，你可能也会看到这样的输出：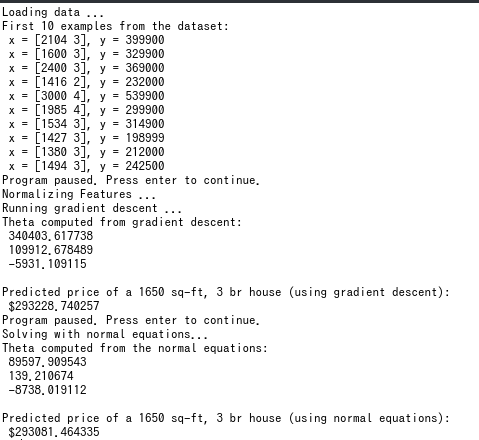
h(x)
　　我们发现，梯度下降得到的答案和标准方程得到的答案有一定的差异。这个应该就算是误差了，当迭代次数越来越多的时候，梯度下降得到的值应该会越来越可靠。从预测值中我们看到，虽然有误差，但其实还可以接受。然而，我们看一下两种方法得到的theta，差别却非常大。这说明了我们用梯度下降算法得到的应该是某一个局部最优解，而这个局部最优解和全局最优解差别很小。