Greedy algorithm & Dynamic programming

Posted on | In | Visitors:
Words count in article: 4.8k

Prologue

　　这是算法导论系列的第二篇笔记，这篇文章的主题是贪心算法和动态规划，主要讲一下两者的思想以及一些简单应用。最后还会将两者做一个简单的对比。当然，贪心和动态规划毫无疑问是算法大家庭中十分重要的两个概念，因此都应该掌握。

Greedy algorithm

　　贪心思想如果用一句话来概括的话，就是不断地寻找局部的最优解以尝试求得全局的最优解。如果把程序看成是一个状态机的话，贪心算法就是找出当前状态下，收益最大的一个转移路径，并跳转到该状态，直到末状态，结束运行。当然，贪心算法并不能保证能得到一个全局最优的解，它需要带求解问题具有最优子结构的特性。利用好贪心思想，可以简化许多复杂的问题。
　　贪心算法的设计步骤如下:

  1. 将最优化问题转化为这样的形式:对其作出一次选择后，只剩下一个问题需要求解
  2. 证明作出贪心选择后，原问题总是存在最优解
  3. 证明作出贪心选择后，子问题满足性质:其最优解和贪心选择组合后可以得到原问题的最优解，即存在最优子结构

Activity selected problem

　　活动选择问题是贪心算法的一个重要应用。假定有一个n个活动的集合\(S=\{a_1,a_2,…a_n\}\)，这些活动使用同一个资源（比如一个教室），而这个资源在某一个时刻只能给一个活动使用。每个活动有一个开始时间\(s_i\)和一个结束时间\(f_i\)，其中\(0\leq s_i<f_i<∞\)
　　如果某个任务被选中，即任务发生在区间\([s_i,f_i)\)中。如果两个活动的区间不重叠，我们称两个活动是兼容的。我们的任务是寻找一个最大的兼容活动集合。
　　首先，我们需要先证明活动选择问题具有最优子结构。用\(S_{ij}\)表示在\(a_i\)结束后开始，且在\(a_j\)开始前结束的活动的集合。我们希望求解的是该集合的一个最大的相互兼容的活动子集。假定\(A_{ij}\)为这样的一个集合，且该集合包含了活动\(a_k\)。那么这个时候我们得到了两个子问题:\(S_{ik}和S_{kj}\)的最大兼容活动子集。可以用剪切-粘贴法证明。这样，我们可以把问题不断地细分:
$$
A[i,j]=\begin{cases}
0,\quad S_{ij}=\phi \\
\max\limits_{a\in S_{ij}}{A[i,k]+A[k,j]+1},\quad S_{ij}\not=\phi
\end{cases}
$$
　　当然，我们还有其他的做法。我们事实上不需要去考虑\(S_{ij}\)区间内所有的活动，直观上，如果我们想要在一个区间内容下更多的活动，那么就要求当前选择的活动能给剩下的活动留下更多的空间。因此，我们可以在\(S_{ij}\)区间内选择结束时间最早的活动。这样我们就可以这样去解决活动选择问题:

1
2
3
4
5
6
7
8
9
Activity-Selector(s,f,k,n)
    n = s.length
    A = {a[0]}
    k = 0
    for m = 1 to n
        if s[m] >= f[k]
            A = A U {a[m]}
            k = m
    return A

　　为了方便求解，我们需要添加一个虚拟的活动，\(a_0\)，其结束时间\(f_0=0\)。我们在把集合S中的所有活动按照开始时间从小到大的顺序排序后，调用Activity-Selector方法就可以得到完整的最大兼容子集\(A_{1,n}\)，最终复杂度为O(nlogn)
　　如何证明这样的选择是正确的呢？我们可以同样可以利用剪切-粘贴法去证明，比较简单，这里就不详细写了。另外，注意到，选择时间最短的活动不一定能得到最大兼容子集，比如活动集合\(S={a_1=[1,9),a_2=[8,11),a_3=[9,15)}\)，时间最短的活动并不在最大兼容子集当中。那么如果选择开始时间最晚的活动呢？其实也是可以的，不过我们就需要从右往左去遍历了，同时按照结束时间去排序。

Huffman coding

　　贪心算法的另一个应用就是赫夫曼编码，这种编码可以有效地对数据进行压缩。具体的压缩率和数据相关。如果我们把待压缩数据看作字符序列(8位二进制数)，根据每个字符的出现频率，赫夫曼贪心算法构造出各个字符的最优二进制表示。
　　考虑大量字符序列，假设字符a的出现频率很高，那么如果我们能够减小a的二进制表示长度的话，我们就可以对数据进行很好压缩。赫夫曼编码就是这样做的。对于出现频率越高的字符，它的字符编码越短，反之越长。比如对于这样一个文件:
$$
\begin{array}{|c|c|c|c|c|c|c|}
\hline
& a & b & c & d & e & f\\
\hline
频率(千次) & 45 & 13 & 12 & 16 & 9 & 5\\
\hline
定长编码 & 000 & 001 & 010 & 011 & 100 & 101 \\
\hline
变长编码 & 0 & 101 & 100 & 111 & 1101 & 1100 \\
\hline
\end{array}
$$

　　使用定长编码，我们需要30W个二进制位来编码文件。如果使用变长编码的话，我们只需要\((45 \times 1+13 \times 3+12 \times 3+16 \times 3+9 \times 4+5 \times 4) \times 1000=22.4W\)个二进制位，节约了大概 25K 的空间。下图a为定长编码的编码树，b为变长编码。

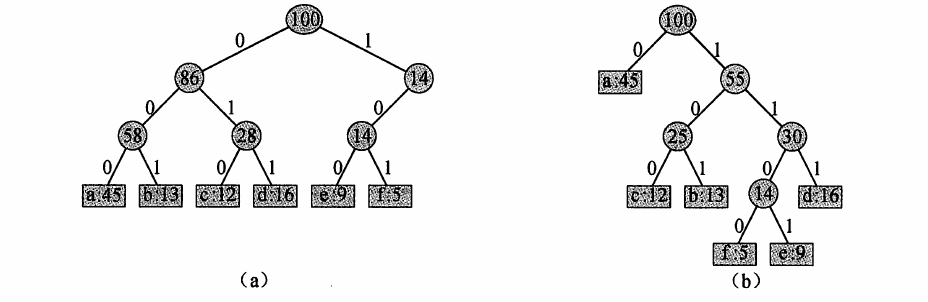
huffman

　　文件的最优编码方案总是对应一棵满二叉树。即每个非叶结点都有两个孩子。给定一棵对应前缀码的树T，我们可以很容易算出编码一个文件 需要的二进制位的个数。对于每个字符c，令c.freq表示字符在文件中出现的频率，\(d_T(c)\)表示c的叶结点在树中的深度(同时也是字符c的码字的长度)。则编码文件需要的二进制位数量为:

$$B(T)=\Sigma_{c \in C}c.freq*d_T(c)$$

　　我们称B(T)为T的代价
　　赫夫曼编码就是使用贪心思想，构造出一棵最优的前缀树对文件进行编码。具体的做法如下:

1
2
3
4
5
6
7
8
9
10
11
// C为字符集合
// Q是最小堆，初始包含n个字符对应的频率
Huffman(C)
    n = |C|
    for i = 1 to n-1
        z = new node()
        z.left = x = Extract-min(Q)
        z.right = y = Extract-min(Q)
        z.v = x.v+y.v
        Insert(Q,z)
    return Extract-min(Q)

　　我们每次从堆中拿出频率最小的两个元素，将它们合并成一棵树，然后再把树根重新扔进堆中。最后，我们就得到了霍夫曼编码的前缀树了。算法导论的图如下: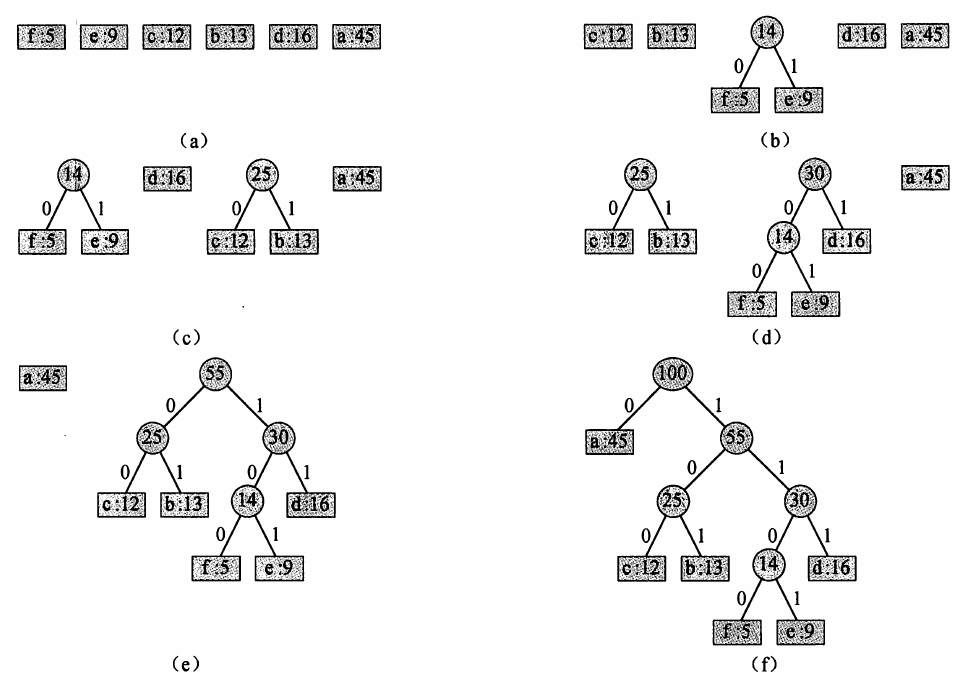
huffman
　　看起来霍夫曼编码的实现似乎挺显而易见，然而正确性又该怎么证明呢？书中给出的证明方法是这样的:

　　引理1：令C为字符集，其中每个字符c都有一个频率c.freq。令x和y是C中频率最低的两个字符。那么存在C的一个最优前缀码，使得x和y的码字长度相同，且只有最后一个二进制位不同
　　证明方法是令T为任意一个最优前缀编码树，x和y频率最低的两个字符对应的结点，a和b是深度最大的兄弟叶结点。不妨假设a.freq<=b.freq且x.freq<=y.freq，由于x和y频率最小，我们有x.freq<=a.freq且y.freq<=b.freq。那么交换x和a，得到的新树T’和原树T的代价差为:
$$
\begin{align}
A =& \, x.freq \ast d_T(x)+a.freq \ast d_T(a)-x.freq \ast d_{T’}(x)-a.freq \ast d_{T’}(a)\\
=& \, x.freq \ast d_T(x)+a.freq \ast d_T(a)-x.freq \ast d_T(a)-a.freq \ast d_T(x)\\
=& \, (a.freq-x.freq) \ast (d_T(a)-d_T(x))\\
\geq & \, 0
\end{align}
$$
　　引理2：令C为字符集，其中每个字符c都有一个频率c.freq。令x和y是C中频率最低的两个字符。令C’为C去掉字符x和y，加入一个字符z后得到的字母表。类似C，也为C’定义freq，其中z.freq=x.freq+y.freq。另T’为字母表C’的任意一个最优前缀码对应的编码树。于是我们可以将T’中叶子结点z替换为一个以x和y为孩子的内部结点，得到树T，且T表示字母表的一个最优前缀码
　　由引理1和引理2，我们可以成功地证明霍夫曼编码可以获得一个最优前缀码。
　　另外，由霍夫曼编码的构造方式，我们可以证明。对于一个由8位字符组成的数据文件，若256个字符的频率大致相同(最高的频率低于最低的两倍)，霍夫曼编码并不比8位固定长度编码方式更加高效。由此继续可以证明，对于一个随机生成的8位字符组成的文件，没有任何压缩方法可以将其压缩！

Matroid

　　在贪心算法后，书中还提到了一种特殊的理论——拟阵。这种理论描述了很多贪心算法生成最优解的情形，并且覆盖了很多其他应用。
　　拟阵是一个满足这种条件的序偶\(M=(S,{\mathcal{I}})\):

  1. S是一个有限集
  2. \({\mathcal{I}}\)是S的子集的一个非空族，这些子集为S的独立子集，使得如果\(B \in {\mathcal{I}} 且 A \subseteq B\)，则\(A \in {\mathcal{I}}\)。我们称\({\mathcal{I}}\)是遗传的。注意，\({\mathcal{I}}\)必然包含空集。
  3. 若\(A \in {\mathcal{I}}，B \in {\mathcal{I}}且|A|<|B|\)，那么存在某个元素\(x \in B-A 使得 A \cup {x} \in {\mathcal{I}}\)。即M满足交换性质。

　　简单来说，条件2即为:若T是S的某一个独立子集，则T的子集同样是S的独立子集。条件3保证了所有的最大独立子集(即再添加元素后就不满足独立性)的大小是相同的。这是拟阵很重要的两个性质。另一个很常见的拟阵的例子是图拟阵\(M_G=(S_G,{\mathcal{I_G}})\)。它定义在一个给定的无向图\(G=(V,E)\)上:

  1. \(S_G\)定义为E，即G的边集
  2. 如果A是E的子集，则\(A \in {\mathcal{I_G}}\)当且仅当A中的边不会构成环，也就是说，边集A是独立的当且仅当子图\(G_A=(V,A)\)形成一个森林。

　　下面证明G是无向图(无重复边)时，\(M_G=(S_G,{\mathcal{I_G}})\)是一个拟阵:

  1. 边集\(S_G=E\)显然是有限集，条件1成立。森林的一个子集显然也是森林，故条件2也成立
  2. 对于一个无向图\(G=(V,E)\)，包含了\(t=|V|-|E|\)棵树(可用树中边和点的数量关系证明)。此时，若\(A \in {\mathcal{I_G}}，B \in {\mathcal{I_G}}且|A|<|B|\)，那么森林\(G_A,G_B\)分别包含\(|V|-|A|和|V|-|B|\)棵树。即\(G_B\)中树的数量比A少，B中必然存在某棵树T，其中存在一条边\((u,v)\)，满足\(u,v在G_A\)中属于两棵不同的树。因此将边\((u,v)\)添加进森林\(G_A\)中，能保持森林的性质，不会产生环，故满足了条件3。

　　对于一个图拟阵\(M_G\)，其最大独立子集边数必定为\(|V|-1\)，它连接了所有的顶点，这样的一棵树成为生成树。在拟阵的基础上，我们可以定义一种加权拟阵，即将拟阵与一个权重函数w相关联，每条边x具有一个权重w(x)>0。我们可以计算整棵树的权重:

$$w(A)=\Sigma_{x \in A}w(x)$$

　　利用贪心算法，我们可以求得加权拟阵中权重最大的独立子集。其中一种重要的应用就是最小生成树。给定一个连通无向图\(G=(V,E)\)，每条边e都有权重w(e)，我们希望求得一个边的子集，使得这些边能构成一棵连接所有顶点的树，且权重之和最小。我们可以将这个问题转化为图拟阵的最优子集问题。考虑加权拟阵\(M_G\)，其权重函数为\(w(e)=w_0-w\)，其中\(w_0\)为一个足够大的常数，保证权重函数的非负性质。显然，此加权拟阵的最优子集即为原图的最小生成树的边集。求解最优子集的算法如下:

1
2
3
4
5
6
7
Greedy(M,w)
    A = 空集
    sort(M.S) // 从大到小
    for x in M.S
        if A并x是M的独立子集
            A = A并x
    return A

Dynamic programming

　　动态规划同样是算法系列及其重要的部分。用一句话概括的话，动态规划就是不断的将当前问题划分成多个可解决的小问题，并且满足所有小问题的解能合成当前问题的解。动态规划的求解过程就是一个不断地划分问题的过程。
　　动态规划问题的求解步骤如下:

  1. 刻画一个最优解的结构特征
  2. 递归地定义最优解的值
  3. 计算最优解的值，通常采用自底向上的方法
  4. 利用计算出的信息构造出一个最优解

　　这样写可能还是有点难理解，我们还是直接来看一道简单的题吧。

Matrix-chain multiplication problem

　　矩阵链乘法应该算是动态规划的一个典型例子。给定n个矩阵的序列\(<A_1,A_2,A_3,…A_n>\)，矩阵\(A_i\)的规模为\(p_{i-1} \times p_i\)，求一个完全括号化方案，使得乘积\(A_1A_2A_3…A_n\)所需的标量乘法次数最少。
　　我们知道两个矩阵大小分别为\((x,y),(y,z)\)时，它们能做矩阵乘法，且所需的标量乘法的次数为\(x \times y \times z\)。比如给定三个矩阵的规模为\(A_1=(2,3),A_2=(3,4),A_3=(4,2)\)，如果按顺序相乘，我们所需的乘法次数为\(2 \times 3 \times 4 + 2 \times 4 \times 2 = 40\)，如果我们让后面两个矩阵先进行乘法，我们所需的乘法次数变成\(3 \times 4 \times 2 + 2 \times 3 \times 2 = 36\)。乘法次数变少了!现在我们的问题就是当矩阵的数量变成n时，应该如何编程求解?
　　为了方便起见，我们用符号\(A_{i..j}表示A_iA_{i+1}…A_j\)的结果。显然，如果i<j，我们必须在某一个\(A_k和A_{k+1}\)时间将矩阵链分开。也就是说，我们首先计算\(A_{i..k}和A_{k+1..j}\)，再计算它们之间的乘积，最终我们得到了\(A_{i..j}\)的值。
　　于是，我们得到以下的递归求解方案:
$$
A[i,j]=\begin{cases}
0,\quad 如果 i = j \\
\max\limits_{i \leq k < j} {m[i,k]+m[k+1,j]+p_{i-1}p_kp_j},\quad 如果 i \not= j
\end{cases}
$$

　　将上述的公式转化为伪代码，则我们得到:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
MATRIX-CHAIN-ORDER(p)
n = p.length-1
创建数组 m[1..n 1..n] 和 s[1..n-1,2..n]
for i = 1 to n
    m[i,i] = 0
for l = 2 to n
    for i = 1 to n-l+1
        j = i+l-1
        m[i,j]=无穷
        for k = i to j-1
            q = m[i,k]+m[k+1,j]+p[i-1]*p[k]*p[j]
            if q < m[i,j]
                m[i,j] = q
                s[i,j] = k
return m and s

Sequence problem

　　序列问题是动态规划问题当中一个很重要的组成部分。其中就有这样一道经典的LIS问题:

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度（雷达给出的高度数据是≤50000的正整数），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

　　最长上升子序列(Least-increasing sequence)问题通常有两种写法。第一种是动态规划，复杂度为\(O(n_2)\)。这类问题任务是从一个数组当中选出一个单调递增/递减的子数组。假设数组长度为n，对于当前第i个元素，我们可以得到以该元素为末尾的子数组的最长数组。我们可以得到以下的递归求解方案(以递减为例子):

$$dp[i] = \max\limits_{\forall k,k<i，a[k]>=a[i]}dp[k]+1$$

　　对于第i个元素，我们都要访问i-1个元素，最后的复杂度就是\(O(n_2)\)了。代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int dp[N]; // dp[i]表示第i个元素结尾的子数组的最大长度
int a[N]; // a为输入序列
int fun() {
    int ans = 0;
    for (int i = 0; i < n; i++) {
        dp[i] = 1;
        for (int k = 0; k < i; k++) {
            if (a[k] >= a[i]) {
                dp[i] = max(dp[i], dp[k]+1);
                if (dp[i] > ans) {
                    ans = dp[i];
                }
            }
        }
    }
}

　　然而，这种写法的复杂度过高了，通常情况下，我们会采取第二种做法——贪心。如果我们换一个角度考虑，对于当前的第i个元素，假设dp[i]=p，说明以第i个元素为结尾的子数组最大长度为p，那么前面i-1个元素必然包含一个长度为p-1的子数组。也就是说，\(\exists k < i, dp[k] = p-1\)。采用贪心的思想，我们只需要取满足条件的k中a[k]最大的那个就可以了!
　　…待续

Knapsack problem

State compression

Differences

　　可以看到，贪心算法和动态规划之间的关系是很紧密的。两种在应用的时候，都要求被解决的问题有最优子结构，并且能够子问题能够合成原问题，但贪心算法的要求会更”高”一些。如果单纯应用贪心算法，我们并不一定能得到一个最优解，而动态规划能保证我们会获得一个最优的结果。并且，动态规划的应用范围要比贪心算法更加广泛，分支也有很多，像是序列的题目LCS，LIS，和LCIS，或是背包问题，区间/树上DP，状态压缩类DP，插头DP等。贪心的话往往是要结合具体题目去分析。

Epilogue

　　这篇博客主要是写贪心算法和动态规划算法的一些知识，并对两者做一个简单的对比。后续如果有时间的话，还是会尽量补上的。(咕咕咕

------------- The artical is over Thanks for your reading -------------