序
这是csapp系列的第六篇文章。具体题目请见官网。本文主要讲csapp中的cache lab的一些问题以及解决办法。如果有什么写得不好的地方,欢迎联系我修改(右下角小图标点开即可对话,可能要稍微等一会)。
建议在开始实验以前,先把官方的资料看下。如果有时间的话,也可以看一下web aside里面blocking相关的一些知识,对于理解题目思路有一定帮助。
cache lab
这个实验总共只有两个部分,part A 要求我们写一个cache simulator, 总体来说比较简单,注意好各个指令间的区别就可以了。part B 是要求我们在特定的条件下对矩阵转置进行适当的优化,有一定难度。
主要实验文件
traces 文件夹 存放用于part A测试的一些文件
csim.c 完成part A 需要填写的文件
trans.c 完成part B 需要填写的文件
test-csim 和 test-trans 分别用于对part A 和 part B的测试
driver.py 用于对part A 和 part B 整体进行测试
实验目的:
part A 主要加深了我们对于缓存的理解,要求能够理解最简单的缓存在机器中是怎样实现的,能够解决写入缓存,读取缓存的一些问题。
part B 主要通过优化转置这个任务,加深我们对cache miss的理解,懂得如何尽量减少cache miss 的产生,以提高程序效率。
实验正文
part A
part A 总体没有什么比较好讲的地方。最主要就是确定好数据结构,理解清楚L S M三个指令之间的区别就可以了。不过笔者在这道题上面却卡了特别久,原因在于对于这几个指令的理解不够深,然后没怎么思考就直接写,导致出了一些问题,找bug花了很长时间,最后发现从一开始的思路就错了,于是才推倒重来。
首先,我们需要用到getopt函数来解析命令行参数。这个函数的用法网上有很多,直接搜索就可以找到很多有用的资料,这里不赘述了。
然后,我们来看一下对于四个指令,I指令我们不需要管,可以直接忽略。剩下L S M三个。一个合格的cache应该做到:
- 对于load指令,从内存中读取,首先我们需要判断要读取的地址是否有放在缓存当中,有的话就是cache hits,直接返回。没有的话就是cache misses,这个时候需要从内存中读取,然后我们还要将这个地址及其对应的值放入缓存当中。
- 对于store指令,往内存中写入,首先我们还是需要判断要存储的目标地址是否放在缓存当中。如果有的话,由于我们采用的是write back策略,我们只需要将值存储在cache当中,只有当其要被替换时,我们才将其写入到内存当中。如果没有的话,发生cache misses这个时候我们需要从内存中读取,在放入缓存当中,在缓存中进行修改。
- 对于modify指令,其实就是先执行load指令,再执行store指令。
实验要求我们输出hits,misses, evicts的次数,并不需要保存缓存中每一个block的值,并且,题目保证了load和store的时候不会越过某一个block的边界,进一步使题目变简单。细心的你可能会发现,我们不需要对三种指令分别进行相应操作。load 和 store指令在本题中没有区别。我们可以将这两个指令分别拆分成两个部分:
- search 搜索对应的set块中是否存在缓存,存在的话则cache hits,更新lru后直接返回,否则发生cache misses,进行第二步
- insert 首先判断当前set块中是否还存在空的line,存在的话我们将其填上,然后返回。不存在的话发生cache evicts,这个时候,由于我们不需要管各个地址中的值,只需要更新一下lru和tag即可。
对于modify,由于load如果缓存中不存在的时候,会从内存中找并且放入缓存当中,因此,store指令一定是cache hits。我们相当与只需要执行load,然后hits++即可。
附:lru(least recently use)在本题中用时间戳表示。每读取一个指令时间戳+1。因此可以保证后一个进缓存的或者后一个被访问到的lru一定更大。我们每次替换的时候只需要找lru最小的那个即可。
核心代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20while(fscanf(fs, "%s %llx,%d", is, &address, &size) != EOF) {
if (is[0] == 'I') continue;
address >>= blockSize;
set = address % maxSet;
address >>= setNum;
tag = address;
struct Line* line = sets[set].line;
int m = sets[set].m; // m 表示编号为set中已经用了的行数(m <= E)
if (search(line, m, tag, lru) != -1) hits++; // cache hits 时search返回-1
else {
misses++;
int pos = try_insert(line, m, tag, lru); // try insert 如果有空位,返回-1,没有空位,则返回lru最小的那个值
if (pos != -1) {
evicts++;
evict(line, pos, tag, lru); // 将lru最小的那个line替换掉
} else sets[set].m++;
}
if (is[0] == 'M') hits++;
lru++;
}
part B
这道题总体来说还是挺难的。尤其是64 * 64的那个部分。笔者最后也想不出比较好的办法。在参考了网上的一些资料之后,最终才拿到了满分。当然32 * 32和61 * 67那块还是比较简单的。题目所给的cache的参数为s = 5, b = 5, E = 1,于是我们知道,这是一个直接映射的cache,sets总数为32。记住cache的参数对于题目的解决及其重要。
32 * 32
首先,这道题其实和之前的performance lab很像。不过我们的目的是减少cache misses的次数,而不是减少cpe,因此重心应该放在cache上。我们可以画一个表来表示出各个元素映射到的set编号。由于32byte的block恰好可以放8个int变量,而一行一共有32个,也就是说每一行占用了4个set,8行可以将所有set填满。第九行开始则有重复之前的周期。因此,我们可以采用8 * 8的分块法,尽可能地减少miss数。
当然,如果你直接这样做,你会发现,这样还是通不了,miss数为三百多,而满分是300以内。其实还有一个重要的可以用到的优化(笔者一开始也没有注意到)。
官方给的文档中有提示,我们最多只能用到12个局部变量。而目前我们仅用了4个(四个循环)。还有8个可以用,并且8个还恰好就是一个set能存放的int数,这个时候我们发现,我们可以先将A矩阵中一整个块(8个变量)取出来,放在局部变量当中,然后再逐一赋值给B矩阵中对应的位置,这样可以避免掉很多不必要的miss(A矩阵每一个块最多只会发生1次miss,而且是必要的),避免了A矩阵和B矩阵相互争夺某一个set导致的conflict miss。于是我们就可以成功地将miss数减少到300以内。成功解决。代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int t1, t2, t3, t4, t5, t6, t7, t0;
for (i = 0; i < N; i+=K)
for (j = 0; j < M; j+=K)
for(int l = i; l < i+K && l < N; l++) {
t0 = A[l][j];
t1 = A[l][j+1];
t2 = A[l][j+2];
t3 = A[l][j+3];
t4 = A[l][j+4];
t5 = A[l][j+5];
t6 = A[l][j+6];
t7 = A[l][j+7];
B[j][l] = t0;
B[j+1][l] = t1;
B[j+2][l] = t2;
B[j+3][l] = t3;
B[j+4][l] = t4;
B[j+5][l] = t5;
B[j+6][l] = t6;
B[j+7][l] = t7;
}
61 * 67
为什么要把这个放在这个地方呢?当然是因为这个比较简单了。61 * 67长宽均是质数,很大一定程度上使得miss数会少一些,当然,这也使得很难通过一些优化将miss减少到一个很低的数值。题目要求的miss数是2000以内,其实只要分块的大小选取得当就很简单了。笔者选择的是16 * 8的块,当然,16 * 16的听说也可以。这个比较随意了,就是一个调参的过程而已。理解清楚之后,和前面那道32 * 32的基本没有区别,代码就不贴了,意义不大。
64 * 64
这个应该就是这个lab最难的一个点了。由于每一行有64个int值,因此,每一行需要占用8个set,即4行就可以把set填满。因此,如果还是采用8 * 8的分块的话,第5~8行占用的set和第1~4行是一样的,这就会导致B矩阵每一次取值都是miss。总的miss率会特别高,显然不恰当。
而如果我们尝试这采用4 * 4的分块法呢?很明显,4 * 4可以避免上面的这种情况。然而又带来了另一个问题,4 * 4中cache的利用率太低了,每次读取8个int,最后用到的却只有4个,因此,这种做法最后miss数大概是1600+,离满分还有很大距离。笔者就是在这里想了很久还是不懂。最后还是去网上看了一下一些其他的思路,最后才恍然大悟(但总觉得这道题有点太取巧了)。下面是我最后获得满分的一个思路(如果涉及侵权,请及时联系我删除):
为了使得cache的利用率达到最大,我们还是得采用8 * 8的分块法,但是,同样的又要避免第5~8行和第1~4行发生conflict miss,我们不能一次性对一整列8个数字进行填充。最后我们采用的策略基于矩阵转置以下的性质:
对于任意矩阵A,我们将A的转置矩阵记为AT。对于每一个8 * 8的块,我们可以将其分成4个4 * 4的子矩阵。分别记为A1,A2,A3,A4。对与A的转置操作,我们可以分解为如下: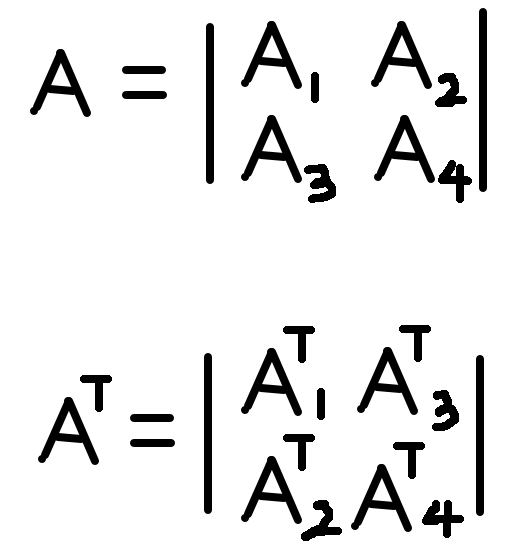
由此,我们可以将整个8 * 8的矩阵的转置分解为以下的三个步骤。
- 对A矩阵的上半部分处理,每次读取A的一行,将A坐上角部分转置后放在B的左上角处,将A右上角转置后放在B的右上角
- 对A矩阵的左下角部分进行处理,按列读取A的右下角中的每一列(4个数字),再按行读取B右上角中的每一行,然后将A读取到的四个数字横放在B的右上角,再将B读取到的四个数字放在B的左下角。本质上其实就等价于将左下角转置后放在B的右上角,将B右上角中上一步得到的数字放在了B的左下角。
- 对A矩阵的右下角部分进行处理,将A右下转置并放到B右下当中
其中,第二步是最关键的部分。为什么这样能够减少miss数呢?如果我们假设4 * 4矩阵平均的miss数为n的话,对于上面三个步骤,我们每一步产生的miss数均大致为n,也就是说,对于一个8 * 8的矩阵,我们的miss数由原先所需的4n降低到了3n。第一步和第三步为n这个很好理解,第二步建议自己再画图理解清楚。最后我们得到的miss数为1100+,而4 * 4的分块约为1600,这也和我们的估计值基本相当。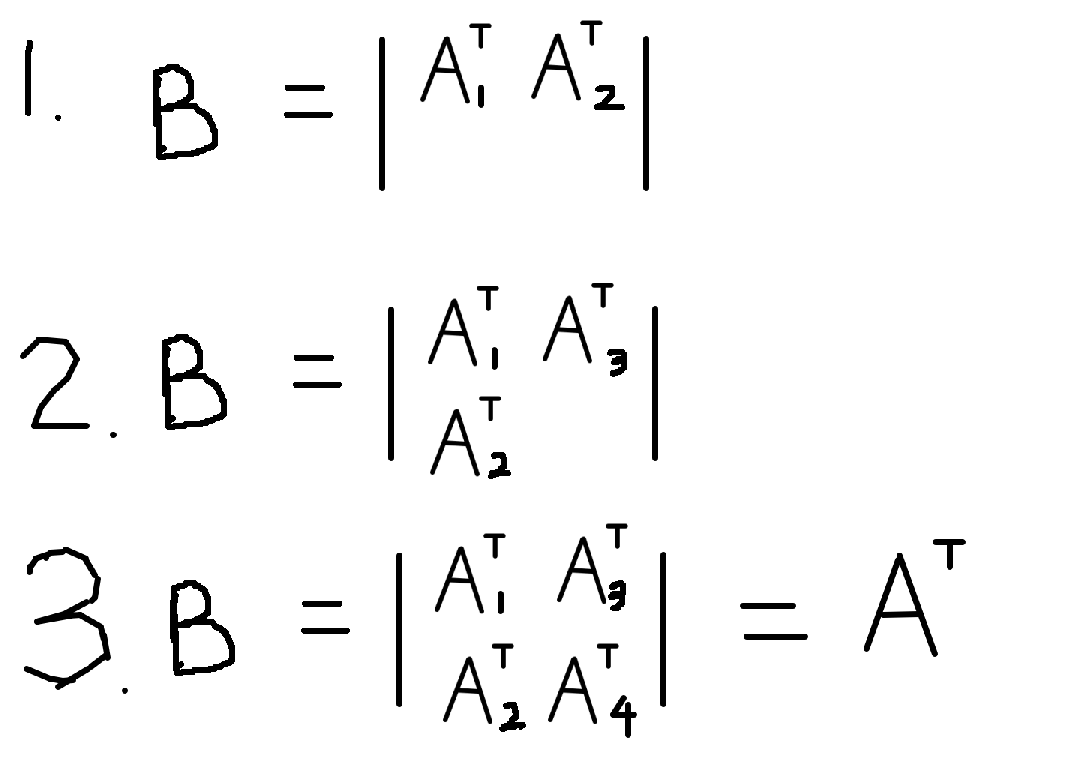
以下是代码,仅供参考:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81int t1, t2, t3, t4, t5, t6, t7, t0;
for (i = 0; i < N; i+=K) {
for (j = 0; j < M; j+=K) {
// 以下循环将A左上转置后移动到B坐上
// 将A右上转置后移动到B右上
for(int ii = i; ii < i + 4; ii++) {
t0 = A[ii][j];
t1 = A[ii][j+1];
t2 = A[ii][j+2];
t3 = A[ii][j+3];
t4 = A[ii][j+4];
t5 = A[ii][j+5];
t6 = A[ii][j+6];
t7 = A[ii][j+7];
B[j][ii] = t0;
B[j+1][ii] = t1;
B[j+2][ii] = t2;
B[j+3][ii] = t3;
B[j][ii+4] = t4;
B[j+1][ii+4] = t5;
B[j+2][ii+4] = t6;
B[j+3][ii+4] = t7;
}
// 将A左下角转置并移动到B右上角
// 将B右上角移动到B左下角
for(int jj = j; jj < j + 4; jj++) {
t0 = A[i+4][jj];
t1 = A[i+5][jj];
t2 = A[i+6][jj];
t3 = A[i+7][jj];
t4 = B[jj][i+4];
t5 = B[jj][i+5];
t6 = B[jj][i+6];
t7 = B[jj][i+7];
B[jj][i+4] = t0;
B[jj][i+5] = t1;
B[jj][i+6] = t2;
B[jj][i+7] = t3;
B[jj+4][i] = t4;
B[jj+4][i+1] = t5;
B[jj+4][i+2] = t6;
B[jj+4][i+3] = t7;
}
// 将A右下转置后移动到B右下
t0 = A[i+4][j+4];
t1 = A[i+4][j+5];
t2 = A[i+4][j+6];
t3 = A[i+4][j+7];
t4 = A[i+5][j+4];
t5 = A[i+5][j+5];
t6 = A[i+5][j+6];
t7 = A[i+5][j+7];
B[j+4][i+4] = t0;
B[j+5][i+4] = t1;
B[j+6][i+4] = t2;
B[j+7][i+4] = t3;
B[j+4][i+5] = t4;
B[j+5][i+5] = t5;
B[j+6][i+5] = t6;
B[j+7][i+5] = t7;
t0 = A[i+6][j+4];
t1 = A[i+6][j+5];
t2 = A[i+6][j+6];
t3 = A[i+6][j+7];
t4 = A[i+7][j+4];
t5 = A[i+7][j+5];
t6 = A[i+7][j+6];
t7 = A[i+7][j+7];
B[j+4][i+6] = t0;
B[j+5][i+6] = t1;
B[j+6][i+6] = t2;
B[j+7][i+6] = t3;
B[j+4][i+7] = t4;
B[j+5][i+7] = t5;
B[j+6][i+7] = t6;
B[j+7][i+7] = t7;
}
}
关于driver.py文件
driver.py是用python语言编写的脚本文件。在做这个任务时,笔者电脑中python的版本是3.7。运行driver.py的时候,出现了异常错误。经打开后发现,这个文件中的python的版本应该是3.0以前的,由于python2.x 和 python3.x的一些语法做了大幅度的修改,因此该文件无法正常运行。如果你也遇到了同样的错误,可以尝试这用以下方法解决:
- 将文件中所有print 后面的表达式加上一个括号。如print “Hello world” 应改为 print(“Hello world”)。python3.0开始就已经不再使用print x这种类型的表达式了。
- 将所有调用到subprocess.Popen函数的式子括号内再加上universal_newlines=True参数。如83~84行应该改为p = subprocess.Popen(“./test-trans -M 61 -N 67 | grep TEST_TRANS_RESULTS”, shell=True, stdout=subprocess.PIPE, universal_newlines=True)
- 89行改为csim_cscore = list(map(int, resultsim[0:1]))
关于前面的archlab-32和performance-lab
这两个实验没有写博客。archlab-32和archlab题目上基本没有什么很大的差别,大体的解决思路类似,因此基本上没有什么重复写博客的必要。然后performance-lab则是因为这个实验难度比较小,没有什么可以写的(虽然这个实验我还是有做的),基本上就是简单的loop unrolling加上分块就可以拿到比较好的分数了。而且题目和Chapter 6的最后两道课后题很类似。这里就不再赘述了。