序
这个系列是关于coursera上吴恩达的machine learning课程的文章。主要内容将包括每个week的编程练习作业,也可能会有一些笔记,知识的整理等,记录下自己学习这个课程的一些心得和体会。本文的主要内容是week 3的编程练习。
关于任务提交,octave的安装中的一些小问题,在上一篇文章中已经有所提及,这里不再赘述。
任务正文
其实上一期任务如果能顺利做下来的话,这一周的任务应该算是很简单的了。基本上照着教程走就没有任何问题了,这里可能着重提一下一些其他的点吧。
需要填写的文件有:
sigmoid.m 对每个元素求g(x) = 1 / (1 + e^(-x))
plotData.m 将数据可视化
costFunction.m 计算代价函数以及梯度
predict.m 对给定的theta和X,计算预测值(0 或 1)
costFunctionReg.m 计算正则化的代价函数以及梯度
plotData.m
这个函数同样的,我们只要照着pdf打即可。注意其中find函数的用法,可以直接获得向量y中所有y=1或y=0的位置
pos = find(y==1);
neg = find(y==0);
plot(X(pos, 1), X(pos, 2), ‘k+’, ‘LineWidth’, 2, ‘MarkerSize’, 7);
plot(X(neg, 1), X(neg, 2), ‘ko’, ‘MarkerFaceColor’, ‘y’, ‘MarkerSize’, 7);
sidmoid.m
按照公式打即可。
g = 1 ./ (1 + exp(-z));
注意’./‘符号作用是用1去除以向量z中的所有元素,得到另一个和z维度相同的向量。exp(x)用于求ex。
另,关于这个g(x)函数,也就是logistic regression和linear regression的一个重要区别。因为在logistic regression,用h(x)表示预测值的话,h(x)的范围应该在(0, 1)当中,且应该是关于y轴上某一点对称。然后我们发现,g(x) = 1 / (1 + e-x)满足了我们所有的需求。当然,这里笔者有个问题,既然我们能采用这个函数来对数据进行转换,我们是不是也可以找到另一个同样满足要求的函数替换掉g(x)呢?
costFunction
在logistic regression中我们用h(x)=g(θTX)代替了h(x)=θTX。并且,我们不再采用平方差的形式,而是使用了log的形式,并且,对于y==0或者y==1的情况的计算公式应该是有区别的,因此,最后采用了这样的计算方法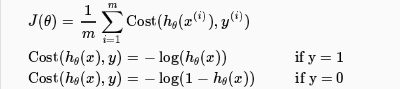
为了更便于我们的计算,我们将这两个公式合并在一起,就变成了下面的公式。当y==0或y==1时,这个公式分别变成了上面的两个公式。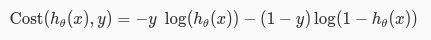
然后,就是关于梯度的计算。和之前的做法其实是一样的。如果不能理解的话还是建议画图。
具体计算方法如下:
z = X * theta;
h = sigmoid(z);
J = -(y’ * log(h) + (1 - y’) * log(1 - h))/ m
grad = X’ * (h - y) / m;
prediction
对于给定的theta和X,我们可以求得当前theta和数据集的情况下θTX的值,我们知道当x大于等于0.5的时候,我们得到的预测值为1,否则预测值为0。由此可以得到以下的写法:
p = sigmoid(X * theta);
p(find(p >= 0.5)) = 1;
p(find(p < 0.5)) = 0;
costFunctionReg
对于正则化下的代价函数,难度稍微增大了一些。
首先是J的计算。和之前相比,现在的代价函数多了一个平方项,由于这一个项的存在,当足够多次的迭代过后,theta总会趋向与0,这就使得在预测函数中,某些项的系数会很快地趋近于0,这样就相当与去掉该项,从而避免了过拟合(overfit)的发生。当然,lambda的值必须取好一点。若取值过大,则会导致前面的log项的作用被稀释,甚至被忽略。最后导致求得的结果连我们给定的数据集都没办法拟合。若取值过小,起不到相应的作用,函数千方百计地拟合我们给定的数据集,使得曲线十分奇怪,过拟合依旧会发生。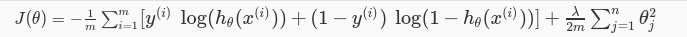

接着,是梯度值的计算。为了向量化计算,这里引入了mtheta变量,其中除了第一个位置以外和theta完全相同,即θ0=0。这样的话,在计算的时候就不会造成影响。注意到正则化是不会对去涉及θ0=0的,笔者一开始在这里没注意,导致预测值出现了问题。
mtheta = theta;
mtheta(1) = 0;z = X * theta;
h = sigmoid(z);
J = -(y’ * log(h) + (1 - y’) * log(1 - h))/ m + mtheta’ * mtheta * lambda / (2 * m);grad = X’ * (h - y) / m + mtheta * lambda / m;
总结
整体上来说,这个练习确实是偏简单了一些,更多的可能是想让我们稍微了解一下该如何去实现某一个特定的算法而已。当然,这个练习中还没有涉及multiple-class的情况,如果有的话,难度应该会更上一层了。接下来下一个周貌似就有相关的练习了,并且将要涉及到Neural Networks的一些东西了。加油吧。