Data Structure Note(I) —— Segment Tree

prologue

　　这是数据结构大杂烩系列的第一篇文章。这个系列主要将记录自己在学习数据结构方面的一些笔记等，以加深自己对数据结构的认识。(不知道能不能坚持做下去
　　在维基百科中，是这样介绍数据结构的：

In computer science, a data structure is a data organization, management, and storage format that enables efficient access and modification. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data.

　　数据结构作为计算机中一个不可分割的重要组成部分，应用十分广泛，几乎在绝大多数的代码中我们都能见到它的身影——链表，栈，队列，树等等。下面就让我们一起来学习一些基础的数据结构吧！
　　今天的主题是segment tree，也就是线段树！

a simple problem

　　在正式学习线段树相关的问题之前，我们先来考虑以下一个问题。

给定一个数组n，然后有m个询问，每个询问包含两个值L和R，我们需要求出在区间[L，R]内所有的元素的和(乘积)。

　　最直接的，我们知道，可以直接起手一个for循环，直接遍历累加即可。好吧，那么这个时候如果n的大小为200000，且有m个询问，复杂度可是O(nm)了，这样的复杂度还能接受吗？作为一个软件工程师，我们当然是不能接受的。那么怎么办呢？
　　这时候你可能要认为，那就用线段树吧，今天的主题。但是，我拒绝！
　　就这个问题来说，我们不需要使用什么数据结构，只需要开一个新的sum数组，对前缀和做一个累加(累乘，不考虑溢出)，然后，我们只需要用sum[R]-sum[L-1]即可得到区间[L,R]的累加值了。
　　这个时候，又来了一个问题，现在我需要修改某一个点x了，这该怎么办呢？直接更新sum[1]~sum[x-1]显然是不行的，这样的效率也太低了，这种方法就做不下去了。这样，我们就引入了一种新的数据结构，叫线段树。

what is a segment tree

　　从名字我们其实就可以猜到它是干什么的。线段树首先是一颗树，而且还是一棵完全二叉树(此处不予证明)。并且，每一个叶子结点的值包含着某一个线段(区间)的一些信息。这就是线段树。这么说可能还有点难以理解，下面我们以一个长度为7的数组[3,4,1,6,7,5,2]为例子，来看下一颗线段树长什么样子。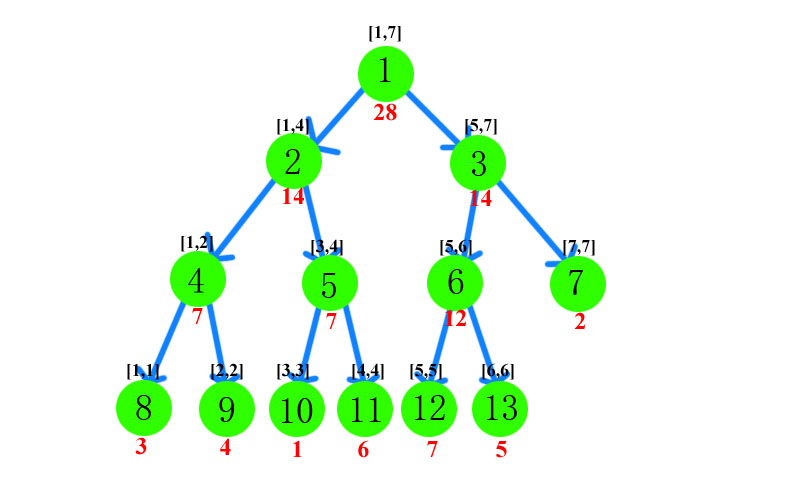
segment_tree1
　　这就是一颗简单的线段树。每个节点包含的区间长度大于1时，则会分裂出子节点，直到长度为1。其中，左儿子为包含的为左半区间，右儿子包含的为右半区间，并且，同一层之间所有节点包含的区间的并集为恰好为整个区间(满二叉树下)，且各节点包含的区间之间没有任何重叠。

struct seg_node {
  int l, r;  // 该节点包含的区间为区间[l,r]
  int sum; // 区间的和
  int maxn, minn; // 区间的最大值和最小值
  ...
} tree[N];

how to build a segment tree

　　构建一颗线段树的话，简单来说就两个字，二分！对于每一个区间[L,R]，当R！=L时，就分裂出子节点，分界为mid。这样，我们就得到了一颗用于求区间和的二叉树。注意到线段树的特性使得对下标为n的节点，左儿子的下标为2n，右儿子的下标为2n+1

#define lson(d) (d<<1)
#define rson(d) (d<<1|1)
int a[8] = [0,3,4,1,6,7,5,2]; // 数组下标是从0开始的，这里为了方便补一个0
void build(int d, int l, int r) {
  tree[d].l = l;
  tree[d].r = r;
  if (l == r) { // 叶子节点时结束递归。并且赋值
    tree[d].sum = a[l];
    return;
  }
  int mid = (l+r)>>1;
  build(lson(d),l,mid);
  build(rson(d),mid+1,r);
  tree[d].sum = tree[lson(d)].sum + tree[rson(d)].sum; // 别忘了递归完后要进行值的合并
}

segment tree’s operation

search one leaf

　　如果我们需要查找某一个节点,我们可以这样来写(其实就是一个二分查找)：

void search(int d, int x) {
  int l = tree[d].l, r = tree[d].r;
  if (l == r) return tree[d].x;
  int mid = (l+r)>>1;
  if (x <= mid) return search(lson(d),x);
  else return search(rson(d),x);
}

　　看到这里，我想也许你会有一个疑问，这样写的话，查找单个点的复杂度不就变成了O(logn)了吗？这效率不是变低了吗？是的，查找一个点的话，效率确实变低了。然而，线段树最大的优势在于区间上！

query

　　接下来这里就是重头戏了，在查找一个区间的时候，我们这样来写：

// 查询[L,R]区间和
int query(int d, int L, int R) {
  int l = tree[d].l, r = tree[d].r;
  if (L <= l && r <= R) {
    return tree[d].sum; // 当所查找的区间完全覆盖当前节点时，直接返回！
  }
  int mid = (l+r)>>1;
  int ans = 0;
  if (L <= mid) ans += query(lson(d),L,R);  // 查找的区间覆盖到左区间时，往左找
  if (R > mid) ans += query(rson(d),L,R);  // 查找的区间覆盖到右区间时，往右找
  return ans;
}

　　下面还是以那个数组为例，看一下查找区间[3,5]的时候会发生些什么(红色的线为查询过程中经过的路径)。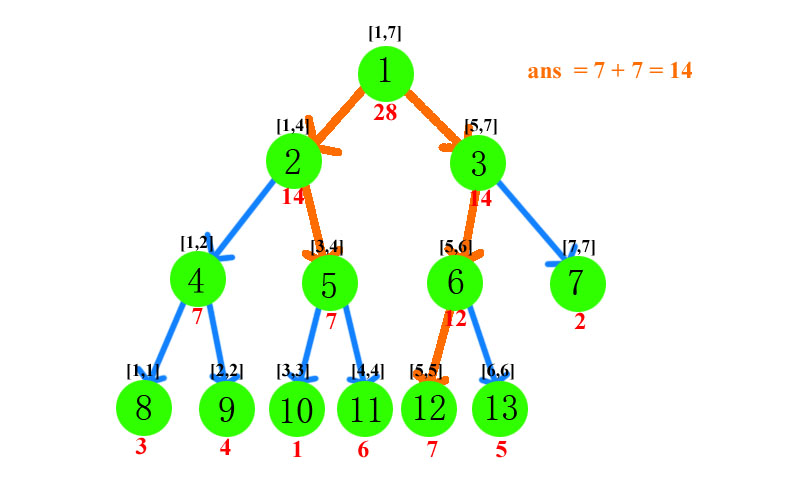
segment_tree2
　　同样的，区间查找也可以用于维护区间的乘积以及最大值和最小值。
　　可以证明，线段树的区间查询复杂度为O(logn)，简单的证明如下：

由前面我们知道，含n个元素的线段树最多为logn+1层。目标证明每一层需要考察的节点数不会超过4个。
假设现在在[l,r]区间内查询[L,R]。在当前层内，考察的节点数为2(左右儿子)。当[L,R]仅覆盖左子区间或右子区间时，递归进入对应区间，下一层考察的节点数仍为2，回到证明2。当同时覆盖左子区间和右子区间时，下一层考察的节点数为4，进入证明3。
将左子区间的左右儿子记为左1和左2，右子区间的左右儿子记为右1和右2。由于区间的连续性和不相交性，查询区间必定覆盖左2和右1，若该区间没有覆盖左1和右2，则下一层需要考察的节点仍然为4个。若区间覆盖了左1，则必然覆盖了左2整个区间，左2不再递归；若区间覆盖了右2，则必然覆盖了右1整个区间，右1不再递归，则下一层需要考察的节点仍然不超过4个。

　　另外一种大致的证明思路是，把当前查询区间[L,R]分为n个子区间，且每一个子区间的长度都是2的整数次幂，即N = 2^k₀+2^k₁+…+2^k_n。且不存在连续的3个k的值相同(若存在，由区间的连续性，则有其中的两个k可以并成一个更大k，矛盾)，故n<=2logN。并且，k的值只能先减小后增大，不会出现两次减小的情况。此时，可以得到每一层需要获取sum的节点数必为常数，最后的时间复杂度级别仍然为O(logn)。

change one leaf

　　尽管前面我们已经能够求得在logn的复杂度情况下求得区间和了，但如果需要修改的话，线段树做的到吗？答案显而易见。当要更改某一个节点时，只需要按照逐层深入，修改某个节点即可,记得修改完后更新父亲节点的值即可。

void update(int d, int pos, int v) {
  int l = tree[d].l, r = tree[d].r;
  if (l == r) {
    tree[d].sum = v;
    return;
  }
  int mid = (l+r)>>1;
  if (pos <= mid) update(lson(d), pos, v);
  else update(rson(d), pos, v);
  tree[d].sum = tree[lson(d)].sum + tree[rson(d)].sum;
}

lazy tag

　　既然前面我们考虑到了改变某个节点，现在如果要更新某个区间呢？线段树又该怎么处理呢？
　　最直接的办法就是逐点更新，这样的处理明显是不行的，但是如果要一次性更新那么多个节点，别说复杂度高达O(mn)，栈也很有可能会爆掉。那么我们有什么好办法呢？
　　注意到一个细节，我们是不是可以不用更新那么多个节点呢？如果只更新少量节点的话，复杂度就可以下降了吧？比如现在在维护一个区间和，然后当前区间为[3,4]，要更新的区间为[2,4]，那么我们是不是可以只要更新节点[3,4]就行了，它的子节点暂时不去管，这样，如果需要查询区间[3,4]，我们也能给出正确的答案，只有当需要请求到[3,3]节点的时候我们再去更新它。如下图：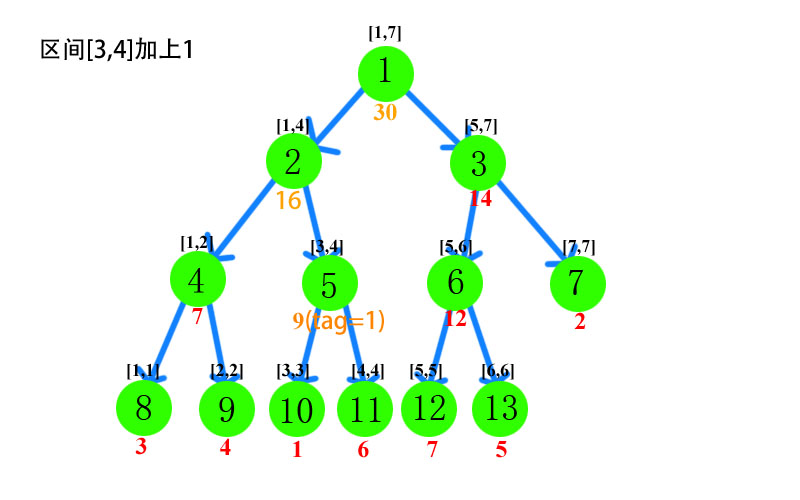
segment_tree3
　　核心代码如下：

struct segment_tree {
    int l, r;
    long long v, tag; // tag为惰性标记，v为区间和
} tree[N];
/* pushdown为线段树的关键操作，作用是将惰性标记从父节点传递到子节点。注意一下，当打上标记tag的时候，
说明当前节点的更新已经完成，但是子节点的值还没有更新。传递的时候就更新子节点，
然后子节点打上标记(子节点的子节点待更新)，并且把当前节点的标记清零，说明子节点的更新已经完成。
*/
void pushdown(int d) {
    int l = tree[d].l, r = tree[d].r;
    int tag = tree[d].tag, mid = (l+r)>>1;
    tree[d].tag = 0;
    tree[lson(d)].v += (mid - l + 1) * tag;
    tree[rson(d)].v += (r - mid) * tag;
    tree[lson(d)].tag += tag;
    tree[rson(d)].tag += tag;
}

void update(int d, int L, int R, int v) {
    int l = tree[d].l, r = tree[d].r;
    if (L <= l && r <= R) {
        tree[d].tag += v;
        tree[d].v += (long long) v * (r - l + 1);
        return;
    }
    if (tree[d].tag) pushdown(d);  // 注意，这行代码不能漏掉，否则会导致当前节点得到的值不是真实值
    int mid = (l+r)>>1;
    if (L <= mid) update(lson(d), L, R, v);
    if (R > mid) update(rson(d), L, R, v);
    tree[d].v = tree[lson(d)].v + tree[rson(d)].v;
}

long long query(int d, int L, int R) {
    int l = tree[d].l, r = tree[d].r;
    if (L <= l && r <= R) return tree[d].v;
    if (tree[d].tag) pushdown(d); // 注意，当想要查询子区间时，需要先进行更新！
    int mid = (l+r)>>1;
    if (R <= mid) return query(lson(d), L, R);
    else if (L > mid) return query(rson(d), L, R);
    else return query(lson(d), L, R) + query(rson(d), L, R);
}

　　线段树一个比较大的难点就在于惰性标记的设置上，一不小心很容易犯错，且通常情况下这种错误很难肉眼直接看出来(笔者就曾经因为惰性标记卡了好久)。这个还是建议做一下题，基本上就可以很好地掌握了。推荐codevs上面的线段树系列。

double lazy tag

　　好了，如果到这里你都能看懂的话，现在难度又要提高了。如果我们的区间更新中，既包括加法，又包括乘法，那该怎么办呢？这样的话，上面的lazy tag做法似乎就存在一些问题了。
　　一个可行的解法是，如果一个lazy tag不行，那就来两个！这样貌似没什么问题，可细细想想，问题老多了。首先，如果有两个tag，一个表示加法，一个表示乘法，那么在传递的时候，我们应该先将哪一个传递下去呢？比如这个时候如果我们对整个区间做了一个加法，又做了一个乘法，再做了一个加法，那这样的话不久乱套了吗？
　　为了顺利解决不同的tag之间的冲突，我们必须为tag定一个先后顺序。
　　让我们先来考虑这样的情况。假设当前区间的和为x，共n个元素，现在依次做一个区间加法a，一个区间乘法b，再来一个区间加法c。
　　如果我们先把加法传递下去。那么第一步打上加法标记a，接下来做区间乘法，打上乘法标记b，再做区间加法，加法标记变为a+c。这个时候进行一次pushdown操作，由于加法优先，子节点(和为x,元素数量为n)从x变为b(x+(a+c)*n)，显然是不对的。如果要使最后的答案变得正确，我们需要把c修正为c/b。这就带来了很多麻烦了。
　　如果我们先把乘法传递下去。一开始打上加法标记a，后面在打上乘法标记b的时候，把加法标记变成ab，最后加上c的时候，加法标记变为ab+c(注意到b*(x+a)+c = bx+ab+c)。即我们需要做的，就是在处理区间做乘法的时候，同时对加法标记做一次乘法，在处理区间做加法的时候，只需要更新加法标记即可。核心代码如下：

struct seg_tree {
    int l, r;
    long long v, add_tag, mul_tag;
} tree[N];
void pushdown(int d) {
    int l = tree[d].l, r = tree[d].r;
    int lson = lson(d), rson = rson(d);
    int mid = (l+r)>>1;
    if (tree[d].mul_tag != 1) {
        long long v = tree[d].mul_tag;
        // 下面取模是题目需要，如果题目保证不溢出，则可省去
        tree[lson].add_tag = (tree[lson].add_tag * v) % mod;
        tree[rson].add_tag = (tree[rson].add_tag * v) % mod;
        tree[lson].mul_tag = (tree[lson].mul_tag * v) % mod;
        tree[rson].mul_tag = (tree[rson].mul_tag * v) % mod;
        tree[lson].v = (tree[lson].v * v) % mod;
        tree[rson].v = (tree[rson].v * v) % mod;
        tree[d].mul_tag = 1; // 注意到乘法标记的初始值应该为1，即乘法运算的单位元
    }
    if (tree[d].add_tag) {
        long long v = tree[d].add_tag;
        tree[lson].add_tag = (tree[lson].add_tag + v) % mod;
        tree[rson].add_tag = (tree[rson].add_tag + v) % mod;
        tree[lson].v = ((mid - l + 1) * v + tree[lson].v) % mod;
        tree[rson].v = ((r - mid) * v + tree[rson].v) % mod;
        tree[d].add_tag = 0;
    }
}

　　当然，如果现在题目不是要求同时做加法和乘法，而是进行set操作(将区间所有值变为一个确定的值，见codevs的线段树练习题)，那么我们的策略也要进行对应的更改，这里不再赘述。另外，说一个题外话，如果有三个或以上的区间操作呢？大体的思路还是一样的，即在保证各个tag不相互冲突的前提下将tag传递到子节点即可。相信聪明的你一定能找到对应的解决办法的。

Binary Indexed Tree

　　前面我们谈到了用线段树去实现区间的修改和查询。但是除去线段树的话，还有没有什么比较好的办法呢？答案肯定是有的，它的名字叫做树状数组。不过，与其说是树状数组，它的英文名字更能体现出它的思想。树状数组的每一个位置存放的是一个区间的值，而不是一个点，其直观表现图如下：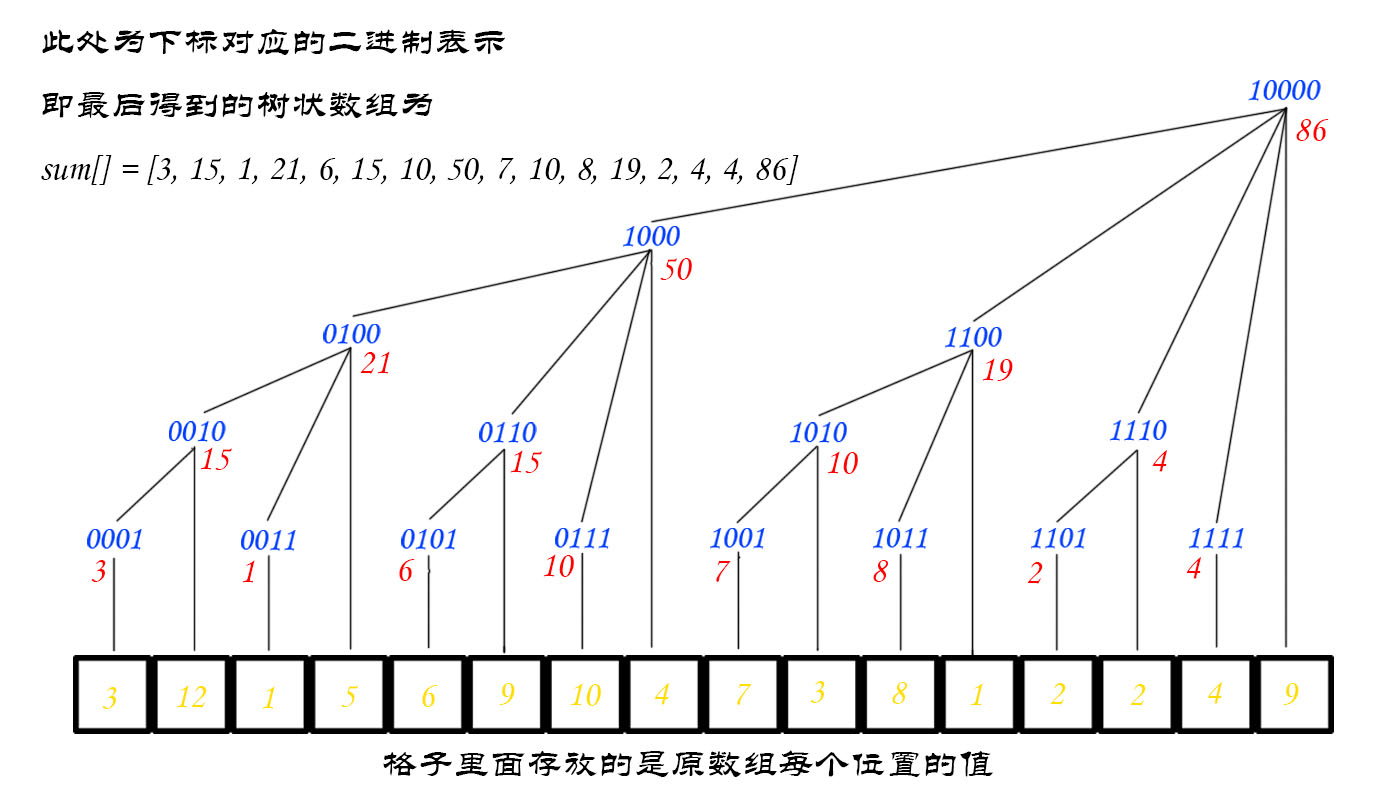
binary_indexed_tree

prepare

　　要实现树状数组，首先，必须要理解lowbit函数，具体如下：

1
2
3

int lowbit(int x) {
  return x&-x;
}

　　尽管只有短短一行代码，理解起来还是有一定难度的。这个函数的作用是取得二进制下x的最小的1所在的位置对应的值。这样说起来有点绕口。举个例子，x=10100100₍₂₎，这个时候x最右的一个1在第三位，对应的值为100₍₂₎。我们可以验证一下，-x = 01011100₍₂₎，x&-x = 100。具体证明此处省略。
　　在理解了lowbit函数后，我们就可以观察上面的图，我们可以看出，每一个点保存的其实就是(x-lowbit(x),x]区间的数字的和。

query

　　理解好了树状数组的结构后，我们来看一下应该怎样对区间进行求和。首先，我们给定x，我们考虑如何求[1,x]区间上所有数字的和。代码很简单，见下：

#define lowbit(x) (x&-x)
// sum[i]为树状数组
int query(int x) {
  int ans = 0;
  while(x) {
    ans += sum[x];
    x -= lowbit(x);
  }
  return ans;
}

　　为什么上面的代码能起作用呢？如果当前我们要查找[1,7]的区间和，那么，由上面的函数，我们可以得到ans = sum[7] + sum[6] + sum[4]。不难看出，对于[1,x]的区间求和的问题，我们可以划分为[1,x-lowbit(x)]和[x-lowbit(x)+1,x]的和两个子问题，而由树状数组的结构，我们有[x-lowbit(x)+1,x]的区间和为sum(x)，这个时候，整个问题就变成只需要求[1, x-lowbit(x)]的值的问题了。这样不断递归下去，最终，当x是2的整数次幂的时候，sum[x]表示的恰好就是[1,x]的值，函数退出，我们成功地求出了前缀和！
　　当我们能求出前缀和的时候，剩下的问题就很简单了。当我们需要求[l,r]的值的时候，我们只需要求query(r)-query(l-1)的值即可。

update

　　我们先来考虑更新一个点的情况。要更新一个点，我们需要同时更新其“父”节点，对于树状数组而言，该节点对应的下标为x+lowbit(x)。由此，我们可以得到以下的函数：

// n 为数组元素的个数
// 注意，对于这种结构的树状数组来说，把点d从a变成b的时候，我们的更新是相当于加了一个差值，即update(d, b-a)
void update(int x, int v) {
  while (x <= n) {
    sum[x] += v;
    x += lowbit(x);
  }
}

　　那么，接下来我们考虑该如何进行区间的更新呢？
　　…
　　…

　　惊了！我们发现，按照我们目前的思路，除了单个点逐步暴力地更新之外，我们发现竟然没有别的什么好办法。那怎么办？这个博客就不写了吗？
　　不，我还是拒绝！
　　其实，想要进行区间的更新还是有办法的，但是我们的数组存放的“东西”得改一改了(见codevs中线段树练习2)。

这里简单的讲一下这道题的意思，就是n个数，m个操作，其中，共有两种操作类型，其一是进行区间的更新(加上某个值)，其二是进行单点的查询。在这样的一个背景下，我们可以使用线段树来完成这个要求。

　　具体来说，对于原先的数组a[N]，我们新建一个数组sum[N]，并且，sum[N]是一个树状数组，保存的是相对与初始值的变化量，初始为空。接下来，更新的操作比较神奇。假设我们要在区间[l,r]上，每个数都加上n。我们知道，下标为x的数字，当且仅当l<=x<=r时，即在区间内时，这个数字需要加上n。这个时候，我们就可以在下标为l的地方加上标记n，在下标为r+1的地方打上标记-n，这样，在单点查询下标为x的位置的值的时候，我们的问题就可以转化为一个区间求值的问题了。如果还是不太理解，请看下图：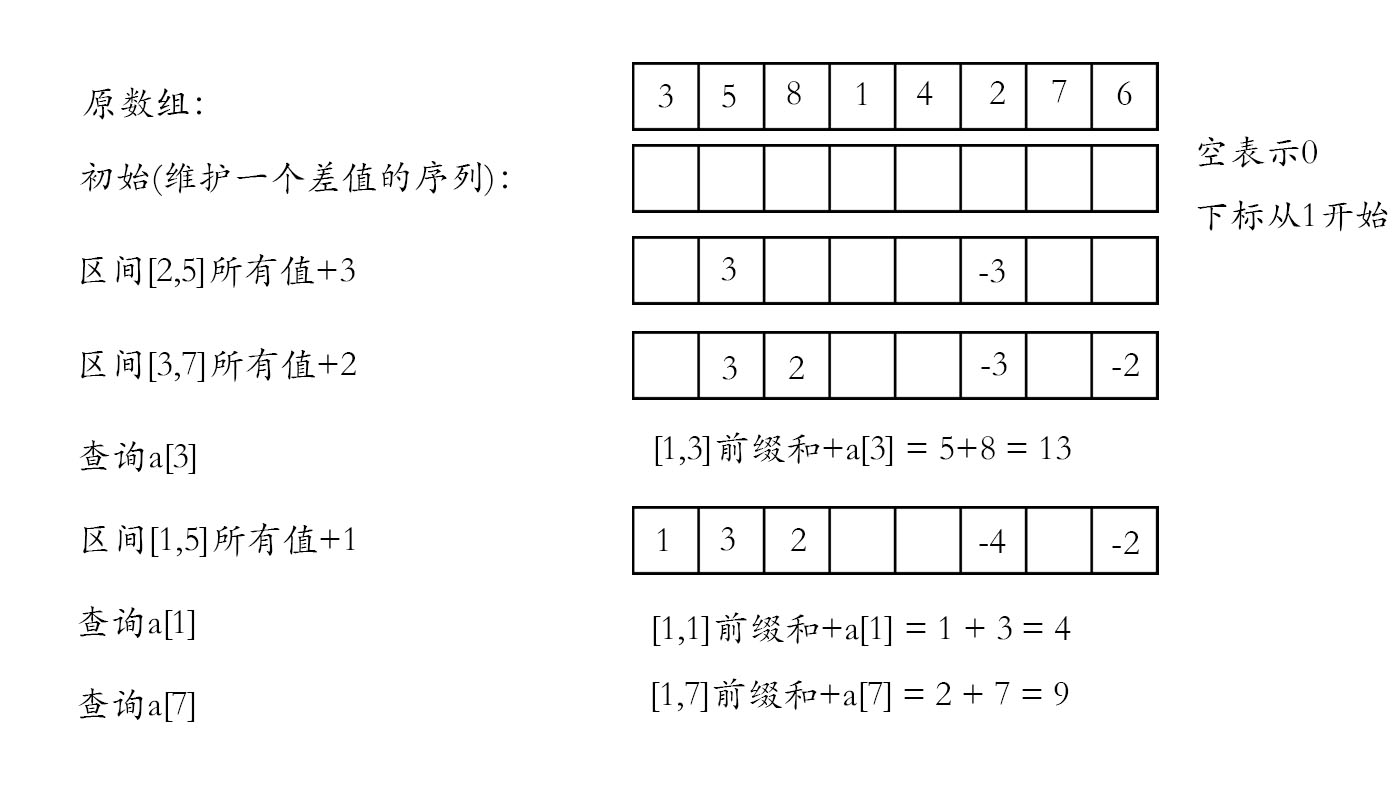
binary_indexed_example

advantage & limitation

　　由上面的介绍，我们其实可以看得出来，树状数组虽然理解起来稍微困难一些，但是代码量是很小的，而且也很难出现一些隐蔽的bug，这对与经常写出bug的程序猿(比如笔者)来说，还是很友好的。并且，时间上，树状数组进行区间查询和单点修改的操作的复杂度为O(logn)，且常数极小，因此在树状数组适用的情景下，其效率是线段树的好几倍(线段树由于存在函数的递归，以及lazy tag的pushdown操作，常数是很大的)。空间上，树状数组通常不需要额外的存储空间，其空间复杂度为O(n)，而线段树通常需要2n~4n的空间，这使得线段树显得过于“笨重”。
　　但是，树状数组的特性也决定了它具有很大的局限性——由上面我们知道，树状数组比较适合用来做区间的查询和单点的更新数量较多的操作，但是无法进行区间的修改。尽管后面的版本我们通过记录区间边界使得树状数组可以进行区间的修改，但同时，无法进行区间的查询，这是相对的。因此，尽管树状数组确实很好用，但应用范围比较狭窄。可以说，树状数组可以实现的东西，线段树都可以实现，然而线段树可以实现的东西，很多情况下树状数组却实现不了。当然，在能用树状数组实现的情形下，还是推荐用树状数组好。
　　另外，关于树状数组和线段树的使用情形，看过一句话说得挺精辟的。在离散数学的观点下，线段树适用于含幺半群(即满足结合律，且有单位元)，而树状数组仅适用于交换群(必须满足结合律，交换律，且含有单位元，以及每个元素均存在逆元)。故树状数组适用范围更小一些。

block(?) algorithm

　　也许上面提供的两种区间的结构化查询你都不够满意，现在，还有一种十分暴力的写法，它的名字叫做”分块”。这种做法就是完全暴力的进行处理，它能处理基本上所有线段树能处理的问题，并且，对于线段树处理不了的某些问题，它竟然也能够处理！那么，我们就来看一看分块是什么吧。
　　现在，我们来考虑下这个问题(codevs的线段树练习4加强版)：

给一个序列，含有n个元素(1<=n<=200000)，要求实现m个操作，共两种类型，第一种是区间每一个数都加上n，第二种是查询区间内有多少个数是k的倍数。其中，1<=k<=200000，1<=m<=200000

　　看到k的取值范围这么大，瞬间慌了，这不就是不想让我用线段树吗？每个节点保存20w个数字，怎么可能？因此，忍无可忍的情况下，我们决定暴力做了。
　　首先，很明显如果我们要直接便利的话，复杂度还是太高了，最坏情况下达到O(mn)，这不行。那么，我们能否参考一下使用线段树的思路呢？具体来说，我们也可以考虑一下将区间分成一个个的小块，然后，维护每一个块上值为1~200000的倍数的数字的数量，这样就可以解决了！
　　以n=200000，1<=k<=200000为例，我们取每一个块的大小为500，那么总共就有400个块，每一个块上维护的话需要400*200000大小的数组。这已经很极限了。当我们需要将区间[l,r]值增加n的时候，按照一下步骤：

l和r在同一个块里面的时候，则r-l<500，我们直接暴力for循环增加即可。
当l和r不在同一个块的时候，不妨假设l所在的块为x1<=l<=x2，r所在的块的范围为x3<=r<=x4，则我们需要for循环更新位于[l,x2]和[x3,r]的所有点的值，并且，将位于x2和x3之间的所有块全部加上标记n即可。这样的话，最坏情况下，复杂度也是近似于O(sqrt(n))。

　　同样的，在进行区间内查询的时候，假设查询[l,r]区间内k的倍数的个数，按照以下步骤：

l和r在同一个块里面，直接暴力求解
l和r不在同一个块里面，则同样假设l所在的块为x1<=l<=x2，r所在的块的范围为x3<=r<=x4。则我们只需要for循环遍历位于[l,x2]和[x3,r]的所有点，看下该值加上当前块的标记值结果是否是k的倍数即可复杂度为O(sqrt(n))。对于位于[x2,x3]内所有的块，假设当前的块标记值为c，则我们只需要查看数组中(k-c)的值即可，复杂度同样为O(sqrt(n))。

　　本质上，这样的分块算法其实相当于一颗高度为3的树，其中，每个非叶子节点的孩子的个数近似为sqrt(n)个。整个问题而言，最后的总复杂度为O(m*sqrt(n))。
　　当然，这道题本身应该有比较优秀的做法，这里只是提一下分块这样的一种思想，在处理一些十分棘手的问题，并且实在想不出什么好的问题的时候，不妨试一试吧。这里顺便说一句题外话，如果是静态的序列，想多次查找某个值是否是k的倍数的话，有一个叫做莫队算法的神奇的东西(好像就是一位叫莫涛的选手发明的)，本质上也是用到了分块的思想。

Range minimum query (RMQ)

　　前面我们提到，树状数组无法实现对于区间的求最值问题，是因为max和min运算不存在逆元。现在，如果我们想求区间的最大值最小值，但又觉得线段树太慢，有没有什么能像树状数组一样快的东西呢？结论是有的！(当然，这种算法不适用于动态更新的序列

detail

　　ST-RMQ算法本质上应该算是动态规划类，它的优秀之处在于，对于一个给定的序列，它只需要O(nlogn)的复杂度进行初始化，此后，能以O(1)的复杂度解决区间最值的求解问题。在一个2^n长度的数组中，对于一个坐标为x的点，我们可以保存以其为起点，且区间长度为2^k的区间的最值。在动态规划的思想中，我们使用F[Bit][Pos]来表示起点位于Pos，且长度为2^Bit的区间的最值。这个时候，求解的状态转移方程如下：

F[bit][p] = max(F[bit-1][p], F[bit-1][p+(1<<(bit-1))]);

　　即对于长度为b = 2^bit的区间来说，该区间的最大值等于两个子区间中最大值更大的那一个。当然，也许你会问，如果仅仅能得到长度为2的幂次的区间的最值，那有什么用？通常情况下，我们遇到的区间的大小都不会是2的幂次。这里有一个比较巧妙的操作。令len是小于等于区间长度的最大的2的幂次，则整个区间的最大值为max(F[bit][l],F[bit][r-len+1])
　　核心代码如下：

// 初始化操作
// max_bit 表示小于等于区间长度的最大的2的幂，下面的bit同理
for (int i = 1; i <= max_bit; i++)
for (int j = 1; j <= n; j++) {
    if (j + (1<<i) - 1 > n) break; // 超过区间的右侧时退出
    int len = 1<<(i-1);
    F[i][j] = max(F[i-1][j], F[i-1][j+len]);  // 状态转移方程
    printf("F[%d][%d]=%d\n", i, j, F[i][j]);
}

// 获取区间[l,r]上的最大值
bit = getLen(r-l+1);
printf("%d\n", max(F[bit][l], F[bit][r-(1<<bit)+1]))

application of setment segment tree

　　前面我们一开始谈到了，线段树是很厉害的，很多事情都可以做。然而，后面我们又枚举了一大堆在比较特殊的情况下，效率比线段树更优的结构，这不是明显打脸吗？现在，我们来看一下线段树究竟可以干一些什么其他的一些结构做不了的事情吧。

discretization

　　为了讲接下来的一个例子，我们需要先提到一个概念——离散化。这是一个很神奇的词汇，它可以将一些看似十分困难的题目转化为一些简单的情形。尽管举的例子不太恰当，但我们还是来看一下下面的一种情形吧。
　　通常情况下，我们建线段树的时候是以数组的下标为叶子节点建立的，比如数组有n个元素，则线段树的叶子节点数量为n。假设我们现在要以值的大小为节点建一个线段树，比如值域为[1,200000]，则线段树有20w个叶子节点，但是，如果值域变为了[1,20000000]，然后元素的个数仅有10000个，这个时候，我们总不可能建一个叶子节点数为20000000的线段树吧。这个时候，我们就需要用到离散化的思想了。
　　离散化思想的本质是，将一个无限大小(或特别大)的空间映射到一个较小的空间。比如下面的函数就类似于一个离散化的过程：

　　再回来考虑我们前面建立线段树的过程，由于只有10000个节点，而值域为[1,20000000]，我们知道各个节点的值的分布是十分“松散”的。这个时候我们就可以使用离散化，具体步骤是将10000个节点按照大小排序，假设排序后的数组为a0,a1…an，这个时候我们取一个映射：a0->1,a2->2…an->n，这样的话，我们就成功地将一个值域为[1,20000000]的离散区域映射到一个[1,10000]的分布较为紧密的区域当中了，这就是离散化。

scan line algorithm

　　这里要介绍的，就是大名鼎鼎的扫描线算法……..的简单版。这就是一个很典型的线段树的应用问题。
　　由于这个笔记的篇幅有点长，这里就不再贴代码了。主要讲一讲相关的思路。为了引入扫描线算法，我们先来看下扫描线算法的一道裸题。

给定一个平面上的n个矩形，求n个矩形的并覆盖到的面积的大小

　　扫描线算法的核心思想在于“扫描”两字，即用一条“扫描线”遍历一整个平面区域。这里，我们假设扫描线与x轴垂直。由于x是递增的，这个时候我们将每一个矩形的两个y轴坐标扔进数组中，进行排序并离散化，映射到一个值域为2n的数组(每一个矩形有两个y坐标)当中，得到2n-1条边，经过去重后，以各条边为叶子节点建立线段树，维护区间的覆盖问题。(其实，关于这里y轴的维护具体实现办法有很多种，比如也可以以每一个y坐标为叶子结点，但实现起来很麻烦，最后还是归结到边的覆盖问题)
　　接下来，具体的做法是：

将扫描线从最左侧开始扫描，在第一次与矩形的边界重合的时候停下。
如果遇到的是左边界，则说明该区间被覆盖。如果遇到的是右边界，则说明该区间不再被对应的某个矩形覆盖。并且更新线段树。
继续往右扫描，直到遇到边界，假设此时前进了deltaX，则当前答案加上deltaX乘上线段树中区间覆盖的面积，再进入2。直到到达最后一条边，结束循环。

　　如果还是不太理解，建议结合下面的图看一下。其中，红色为扫描线，深蓝色表示该边当前已覆盖，浅蓝色表示该边已覆盖。

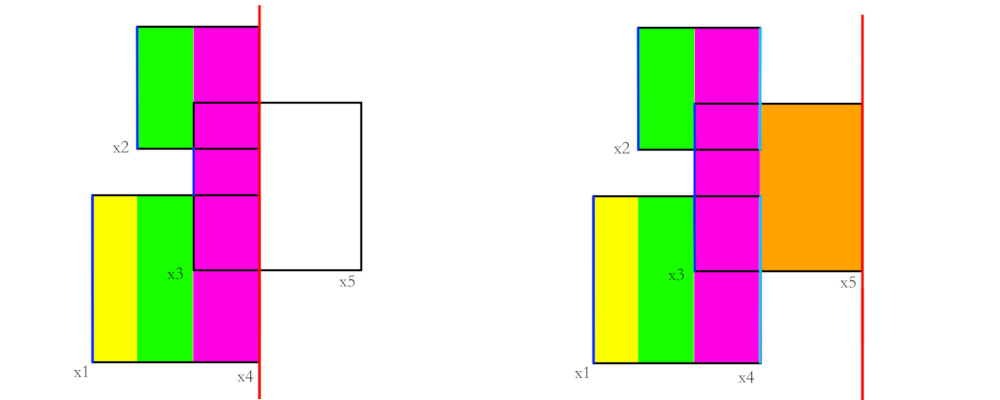
　　这就是实现一个扫描线算法的简单思路，当然，具体实现过程中会有许许多多的小细节，各种边界问题什么的需要处理，难度还是比较大的。这里就不再进行叙述了。(毕竟这是数据结构的笔记，这里提到这个算法主要还是想提一下线段树的应用）

epilogue

　　到这里，我们的数据结构大杂烩系列的第一篇文章就结束了。这里总结一下这篇文章讲的内容吧。首先，由一个简单的问题，我们引入了线段树，并且，讲到了线段树是如何构建的，并且，它是如何实现单点/区间的更新和单点/区间的求和(乘积)，以及线段树的lazy tag思想。在此上拓展开来，我们又简单地提到了树状数组及其应用，这是一种效率很高但同时受限又很大的数据结构，并且我们比较了线段树和树状数组的特点。接下来，我们又讲到了分块算法，在不得已的情况下，我们可能只能采用分块来对区间进行维护，这是一种“暴力”解法的优化版本。接下来，从树状数组的弊端，我们又讲到了在线RMQ算法，这是一种用于多次求解一个固定序列的区间最值的算法，利用到了动态规划的思想。最后，再次回归到了主线，讲线段树的应用问题——扫描线算法，文章也到此结束。

　　由于是刚开始这个系列，感觉写起来还是很乱的，基本上是想到什么写什么，并且，详略上可能也存在一些小问题。这篇文章总共用了一天多的时间，大概是从早上十点多写到晚上十点多吧，第二天也花了好几个小时做一点修改。东西挺多，并且个人感觉也已经挺全面了，不过很多东西仅仅简单提及。当然，本身就不可能做到全面，但还是希望能继续加油吧。

　　预告——下一期应该还是会写和树相关的一些结构，敬请期待吧。