prologue
这是数据结构大杂烩系列的第三篇文章。在前两篇文章中,我们主要学习了线段树,树状数组,以及线段树的可持久化版本(主席树),还稍微提了一下树套树的内容。今天,我们重新换了一个方向——介绍树结构中的另一种及其重要的类型——平衡树。这种数据结构比较难,却很常见(比如set容器),因此我们需要较好地理解与掌握。
a simple problem
我们还是先来看这样一个问题:
给定一个无序数组,查找数字v是否位于数组当中
很显然,遇到这样一个问题,我们最直接的想法就是遍历即可,复杂度为O(n)。但是,如果有多次查找操作的话,一个更好的办法应该是排序,预处理为O(nlogn),然后使用二分查找,单次查询复杂度O(logn),相当不错,但是,如果问题包含了添加和删除操作,那么在每次插入后都要对整体进行排序,效率就比较低了。这个时候我们考虑引入BST。
binary search tree
在正式进入平衡树之前,我们先来看一下一种更基础的结构——二叉查找树(binary search tree)。和它的名字一样,这是一种用于高效查找和插入的基础数据结构,最好情况下,查找和插入的复杂度均为O(logn)。其插入和查找的代码大致如下(其实本质上它就是一个二分查找的过程):1
2
3
4
5
6
7
8
9
10
11
12
13
14// 查找时,如果v大于当前节点,说明v若存在,只能位于右子树当中。
// 同理,v小于当前节点,则只能位于左子树当中。
bool search(Node* rt, int key) {
if (rt == null) return false;
if (rt->v < key) return search(rt—>rson, key);
else if (rt->v > key) return search(rt->lson, key);
else return true;
}
Node* insert(Node* rt, int key) {
if (rt == null) rt = new Node(key)
else if (rt->v < key) rt->lson = insert(rt->lson, key);
else rt->rson = insert(rt->rson, key)
return rt;
}
有了这样的一种数据结构,我们就可以在相当优秀的复杂度的前提下实现动态数组的查询操作,这里不再详细讲述了。但是,普通的BST有个十分致命的缺点,就是它在某些极端数据下,会导致BST退化成了一条链表,比如一个单调递增的数组[1,2,3,4,5,6,7,8],每次插入一个点时,它都会位于上一个点的右儿子,这就导致了整个BST退化。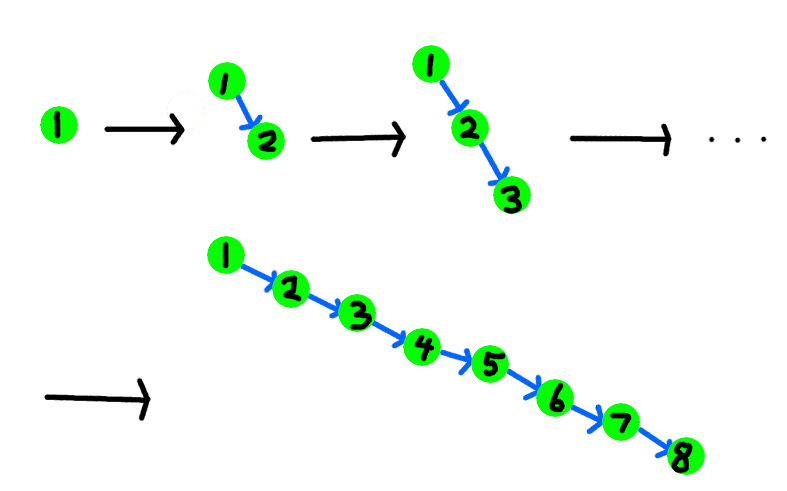
为了解决BST的退化问题,我们需要对原始的BST进行改进,这就产生了平衡树。同样的,和它的名字一样,平衡树和原始的BST相比的特点就是“平衡”,即每个节点的左右儿子大小比较接近,一般就不会有像之前一样的退化成链表的情况了。
treap
Treap是一种实现起来十分方便的平衡树,效率也还不错。Treap是由两个单词组成的,第一个是tree,第二个是heap。tree表明treap是一种二叉搜索树,而heap表明treap同时也满足堆的性质。在这样的背景下,treap实现的期望时间复杂度为O(logn) 。具体treap是怎么实现的呢?答案就是rand()。和普通的BST相比,每个点维护两个值,一个是val,和BST一样,满足二叉搜索树的性质;另外一个是key,或者说是priority,并且满足堆的性质。
rotate
实现treap的最重要的一个操作就是旋转。旋转是平衡树的一个十分重要的操作,通过旋转,平衡树能够在保证满足二叉搜索树的性质的同时,使得左右儿子趋于平衡。代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16// T 表示每一个节点
// rotL表示左旋,rotR表示右旋
inline void rotL(T &t) {
T t0 = t->left;
t->left = t0->right;
t0->right = t;
t->up();t0->up();
t = t0;
}
inline void rotR(T &t) {
T t0 = t->right;
t->right = t0->left;
t0->left = t;
t->up();t0->up();
t = t0;
}
该怎么理解好这段代码呢?以左旋为例,我们来看一下这张图,看下旋转操作究竟发生了什么。(建议自己尝试这画图理解一下)。这是初始状态,其中,我们将1号节点左旋: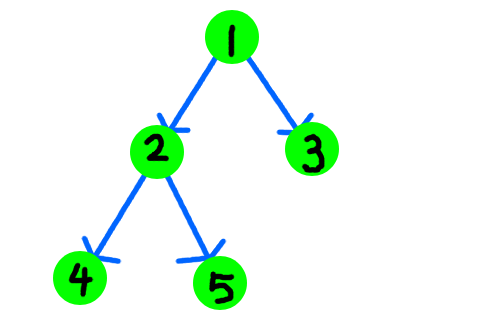
第一步,我们拿到当前节点t的左儿子t0,然后将当前节点t的左儿子指向了t0的右儿子。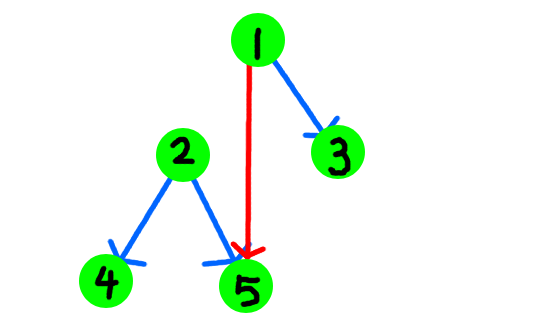
接着,由于t0的右儿子已经给了t,我们此时将t0的右儿子指向了t,这个时候,图像就变成了这样。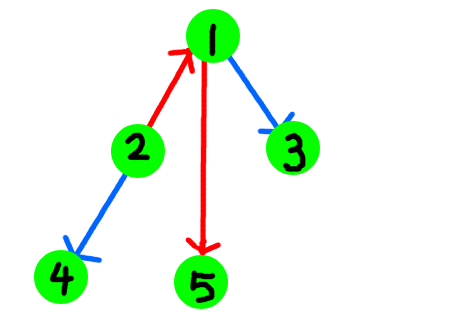
再把图片整理一下,我们发现,之前作为左儿子的t0变成了”根节点”,之前是”根节点”的t却变成了t0的右儿子。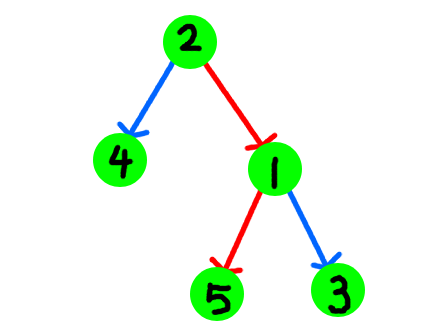
好了,看完左旋操作,我们发现了什么呢?这个操作是不是很像以旋转的目标节点为中心的顺时针旋转操作呢?这就是为什么这个操作被称作左旋,注意到,左旋后,左儿子变成了根。同理,右旋操作会将右儿子变成根,同时,之前的根变成了之前的右儿子的左儿子。虽然有点绕,但还是要理解清楚的。
与此同时,我们发现了一个细节,旋转之前,根的左儿子的高度为2,右儿子的高度为1;旋转过后,根的左儿子的高度变成了1,右儿子的高度变成了2。结合上图,我们可以得知,左旋操作使得当前节点的左儿子高度-1,右儿子高度+1,右旋操作则反过来。因此,通过这样的旋转,我们能使整棵树趋向于平衡状态,这就是平衡树!
旋转操作仅有这些特点吗?显然不止。如果我们把节点的val和priority写上,我们还会发现一个特征。如下图(val简写为v,priority简写为p):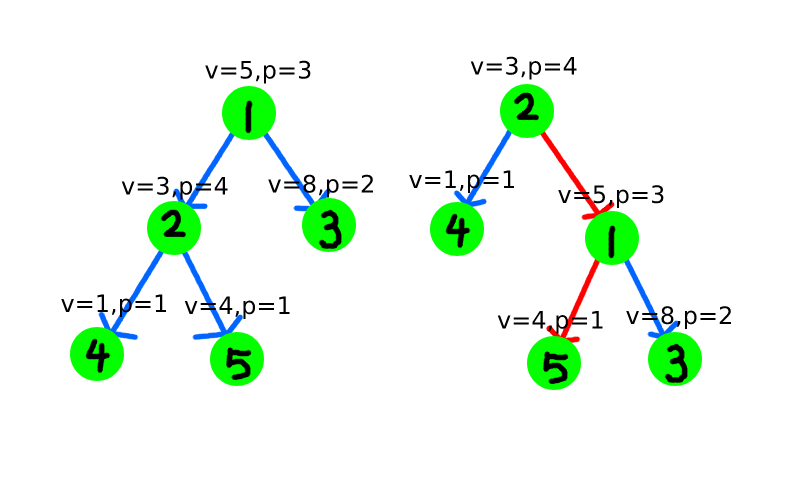
我们先看val的值。仔细观察,我们发现,旋转前,这颗树满足二叉搜索树的性质,旋转后,这颗树依然满足二叉搜索树的性质。即,旋转不破坏BST性质。这是可以证明的,读者不妨自己试一试。
接着,我们再来看一下priority的值,我们发现,在一开始的时候,priority的值不满足堆的性质,但是在左旋过后,priority的值满足了大根堆性质。这告诉了我们,旋转可以用于维护大根堆的性质,当仅有左儿子的priority大于当前节点的时候,我们可以通过左旋操作,使整棵树重新满足了堆的性质。
insert & remove
能理解好treap的旋转操作的话,插入和删除其实就简单很多了,这里以bzoj3224为例,简单介绍一下插入和删除的一般写法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
struct Node {
// left right分别为指向左右儿子的指针
Node *left, *right;
// v为权值,w用来表示出现的次数,即相同的v的个数,减少新建节点的操作
// p表示priority,size维护树的大小
int v, w, size, p;
Node(int v, T k):v(v) {
left = right = k;
p = rand();
w = size = 1;
}
inline void up() {
size = left->size + right->size + w;
} *rt, *empty;
// rt表示root,即根节点,empty表示空节点,用来代替NULL,可以避免对空指针造成某些奇怪的意外
};
void insert(T &t, int v) {
// 指针为空时,新建节点并且返回,注意到参数为&t
if (t == empty) t = new Node(v, empty);
else {
// v相同时累加即可,值小于当前节点,往左儿子插入,大于时往右边插入。
// 注意到插入过后有可能无法满足priority的大根堆性质,需要使用旋转操作来维护。
if (v == t->v) t->w++;
else if (v < t->v) {
insert(t->left, v);
if (t->left->p > t->p) rotL(t);
}
else {
insert(t->right, v);
if (t->right->p > t->p) rotR(t);
}
t->up();
}
}
void remove(T &t, int v) {
// 删除时同理,小于的话往左儿子删,大于的话往右儿子删
if (v < t->v) remove(t->left, v);
else if (v > t->v) remove(t->right, v);
else {
// w大于1时,-1即可。否则删除当前节点。
// 注意到删除节点的时候,如果左右儿子其中一个为空的时候,直接用儿子代替自己即可。
// 如果左右儿子均为空,直接删除即可。
// 如果左右儿子都非空,那么就可以通过旋转操作将儿子移动到当前节点,并递归删除
// 注意旋转时要保证大根堆的性质,另外,new的对象记得回收
if (t->w > 1) t->w--;
else {
if (t->left != empty && t->right != empty) {
if (t->left->p > t->right->p) {
rotL(t);
remove(t->right, v);
} else {
rotR(t);
remove(t->left, v);
}
t->up();
} else {
T t0 = t;
if (t->left == empty) t = t->right;
else t = t->left;
delete t0;
}
}
}
if (t != empty) t->up();
}
其实,插入和删除操作和普通的BST是很像的,区别仅在于treap需要维护大根堆的特性,因此需要有rotate这样的操作来保证。换句话说,treap相比BST仅仅多了priority属性。当然,如果你足够细心的话,会发现treap的平衡性的维护事实上并不是稳定的,因此,treap属于弱平衡树,在某些情况下它的效果不是很好。当然,treap的最大优势在于写法比较简单,并且在实践中的整体表现也较为良好。因此是平衡树的不二选择
no rotation treap
前面我们讲的是普通的treap,它是采用旋转操作来维护priority的,但是,还有另一种类型的treap,它的实现完全不需要旋转,还能维护treap的性质,这就是无旋treap。并且重点是,无旋treap还能用于维护区间,并且支持可持久化。这是多么强大的能力!就让我们一起来学习一下吧。
既然无旋treap不是使用rotate来维护,那么它是怎么保证treap的平衡的呢?这就涉及它的两个核心函数了——split和merge。
split
和字面意思一样,split函数用于把一棵树分裂成两个部分。其中,l,r充当返回值的作用(也可以用pair类,返回两个值),即返回分裂成功的两颗树的根。t是当前待分裂的树,v是用于分裂条件的判断的,此处v表示的是节点的值(我们知道节点的值满足二叉搜索树的性质),v也可以用来表示需要分裂出的子树的大小,这里以按值来分裂为例子。如果v小于等于当前的值,那么说明和v相等的值只会位于左子树当中,则分裂左子树,得到分裂成功的两个子树a和b后,当前节点的左儿子应该指向子树b,并作为右节点返回给上一层,这里需要理解清楚,v大于当前节点时,处理方法同理。递归的边界条件为当前节点是空的,直接返回两个空的子树即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18// 结构体的定义和之前一样。
void split(T t, int v, T &l, T &r) {
if (t == empty) {
l = r = empty;
return;
}
if (v <= t->v) {
split(t->l, v, l, r);
t->l = r;
r = t;
} else {
split(t->r, v, l, r);
t->r = l;
l = t;
}
t->up();
}
如果还是不太理解的话,可以参考一下下面的图。节点中的值表示val。现在执行以下的函数:1
2T a;T b;
split(rt, 4, a, b);
这个函数的结果是把当前的树rt中按照是否小于4分成了两个子树,其中,子树a的所有值小于3,b中的所有值大于等于4,不妨自己手动画一下。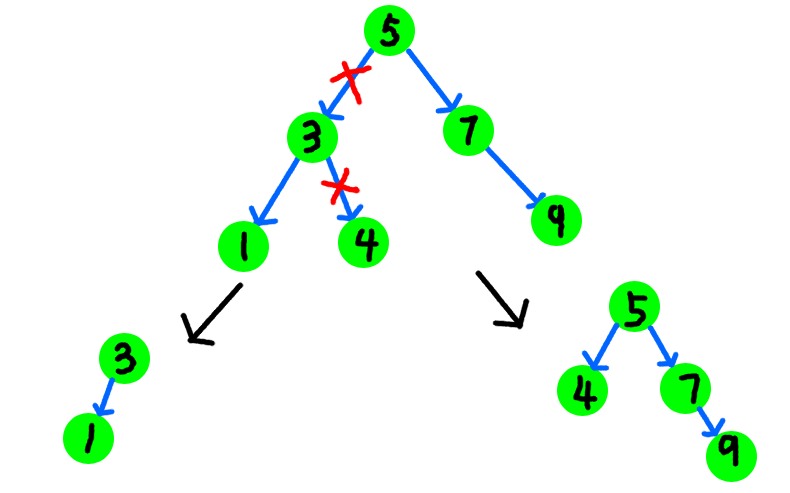
merge
同样的,merge函数用于将两个子树合成为一个。注意到一个重要的事实,合并的两个子树a和b满足a中所有元素的值小于b中所有元素的值。我们考虑一下合并两个子树应有的操作。如果子树a的根节点的priority大于子树b的根节点,那么a应该作为合并后的树的根节点,这个时候,我们就将a的右儿子和b合并(因为b所有元素的值大于a,要满足BST的性质) 。否则,将a和b的左儿子合并。这里要注意参数传递的顺序,不能弄反了。递归的边界条件为子树a或b其中某一个为空,这个时候返回另一个非空的子树即可。(其实,你会发现,无旋treap只有在这个地方用到了priority,因此,即使把a->p > b->p替换成rand()&1也是可以的。这样,就相当于每次合并都是近似随机的了。1
2
3
4
5
6
7
8
9
10
11
12
13T merge(T a, T b) {
if (a == empty) return b;
if (b == empty) return a;
if (a->p > b->p) {
a->r = merge(a->r, b);
a->up();
return a;
} else {
b->l = merge(a, b->l);
b->up();
return b;
}
}
insert & remove
现在考虑我们应该如何插入一个节点。如果我们理解了split和merge操作的话,插入一个节点是很简单的。考虑插入的节点的val为v,那么我们可以将当前的树用split划分成为小于v和大于v和等于v的三个部分a,b,并且把当前节点c看作一颗独立的树,依次将a,c,b合并成一颗树即可。1
2
3
4
5
6
7
8
9
10
11
12void ins(int v) {
T a;T b;
T c;T d;
split(rt, v, a, b);
split(b, v+1, c, d);
if (c == empty) c = new Node(v, empty);
else {
c->w++;
c->size++;
}
rt = merge(a, merge(c, d));
}
删除操作其实也是很类似的。我们同样将原来的树划分为三个部分。并且,得到的等于1的那个部分如果w大于1,直接减1就好。否则就直接将小于v的子树和大于v的子树合并。1
2
3
4
5
6
7
8
9
10
11void rem(int v) {
T a;T b;
T c;T d;
split(rt, v, a, b);
split(b, v+1, c, d);
if (c->w > 1) {
c->w--;c->size--;
d = merge(c, d);
}
rt = merge(a, d);
}
当然,读者如果细心的话,会发现这里其实忘记回收节点了,这个就导致了内存泄漏了鸭(雾
build a treap
至于建立一颗treap的话,方法其实有挺多种,其中一种就是直接把每一个节点按顺序插入即可。另一种方法就是对插入的数组进行二分建树,复杂度也差不多。当然,如果是维护一个区间的话,我们可以采用笛卡尔树的建树方法,复杂度仅为O(n)。这里就不再赘述了。
maintain an interval
和普通的treap相比而言,无旋treap的一个重要用法是维护一个区间。如果现在给定一个数组a = [1,7,3,5,6,4,2],现在以数组下标为val建树,则我们得到的树当中,对于任意一个节点,当前节点的左儿子在数组中下标一定在当前节点左侧,右儿子在数组中的下标一定在当前节点右侧,并且,每一个节点的构成的树包含的是一个连续的区间!这是一个及其重要的性质,利用这个性质,我们可以做到很多意想不到的事情,以noi2005维修数列为例。无旋treap可以动态地维护一个区间,某种程度上有点像线段树!
题目的大题意思如下:
维护一个数列,要求支持添加,删除,翻转,修改,求和,求最大子序列和这几种操作
其中,添加和删除是很简单的,前面已经讲过,这里不再赘述。至于求和操作,我们可以在每一个节点当中存一个值用来维护子树的大小。翻转操作的话,我们可以为每个节点打上一个标记,然后仅反转左右儿子即可。最大子序列的维护方式其实和线段树的处理方法是很类似的。每个节点维护当前节点包含的区间内左端点开始的最大值,右端点开始的最大值,以及整个区间的最大子序列,这样就可以用1
2
3
4sum = l->sum + r->sum + v;
lsum = max(l->lsum, max(l->sum + v, l->sum + v + r->lsum));
rsum = max(r->rsum, max(r->sum + v, r->sum + v + l->rsum));
msum = max(max(l->msum, r->msum), max(l->rsum, 0) + v + max(r->lsum, 0));
来维护最大子序列了,其中,msum是区间的最大子序列,lsum是从左端点开始的最大子序列,rsum是从右端点开始的最大子序列。限于篇幅,这里就不再详细展开了。但是强烈建议读者亲自去尝试实现这道题,基本上能解决这道题的话,可以说就算是基本掌握无旋treap了。
persistability
这里再简单补充一下。我们前面说,treap可以实现可持久化,那么,应该怎么实现呢?我们考虑一下之前线段树我们是怎么实现可持久化的——动态加点。因此,treap也可以用类似的思想去实现。我们每一次新的操作的时候,对每一个点都拷贝一份新的,然后就可以”复用”之前建立的树的信息了。但是一定要记住,后面的操作不能修改前面建立的树,否则可持久化特性就会被破坏。这也是为什么旋转treap不适合用于可持久化——旋转操作破坏了父子关系顺序。
具体实现过程中,我们可以写一个copyNode的复制函数(如果使用结构体和指针写法的话,可以new一个节点然后直接赋值即可):1
2
3
4
5
6
7
8int copyNode(int rt) {
int cur = ++tot;
ch[cur][0] = ch[rt][0];
ch[cur][1] = ch[rt][1];
sz[cur] = sz[rt];
... // 信息的复制
return cur;
}
然后每一次需要更改节点的信息的时候,复制一个新的节点,在新的节点上修改信息即可,比如pushdown操作,split操作和merge操作。参考题目:可持久化文艺平衡树。
summary of treap
这里来对treap进行一个简单的总结吧。两种treap其实算是各有优势吧。第一种treap利用旋转维护priority,由于rand的随机性,我们能够实现一个效率比较高的简易平衡树。第二种treap利用的是分裂和”随机”合并操作来实现平衡的。第一种做法的优点在于它的写起来确实比较简单,并且它的常数较小。而第二种方法的优点在于能够实现区间的维护操作,并且能可持久化,写起来也比较简单。对于treap来说,无论是插入或者删除,查询等操作,其复杂度都是O(logn),基本上算是相当优秀了。但是,treap始终是”伪”平衡树,有时候会被某些极端数据卡。
splay
前面我们介绍了treap,它确实很好用。然而,还有另外一种常用的平衡树,叫splay,中文名称为伸展树,很好地说明了这种平衡树的特性。和treap不同,splay在实现平衡的时候并不是为每个节点赋优先级,而是使用了”伸展”操作。
并且,splay在实现的时候,需要多记录一项每一个节点的父亲,用于后面的操作。
rotate
在splay中,同样有旋转操作,不过这里的旋转操作的定义和treap不太一样。我们先来看一下splay是怎么进行旋转操作的吧。以下为伪代码:1
2
3
4
5
6
7
8
9
10
11
12// up为每个节点的更新操作,类似treap,注意顺序。
// ch[x][0] 表示x的左儿子,ch[x][1]表示x的右儿子,fa[x]表示x的父亲
void rotL(int x) {
int y = fa[x], z = fa[y];
ch[y][0] = ch[x][1];
fa[ch[x][1]] = y;
ch[x][1] = y;
fa[y] = x;
fa[x] = z;
if (z) ch[z][y == ch[z][1]] = x;
up(y);up(x);
}
如果仔细地画一下的话,我们会发现,splay的旋转操作事实上是每个点向上旋转的,传进去的参数是需要”向上走”的点,而treap有点像是向下旋转的,传进去的参数是需要”向下走”的点,这是两种平衡树的一个重要区别。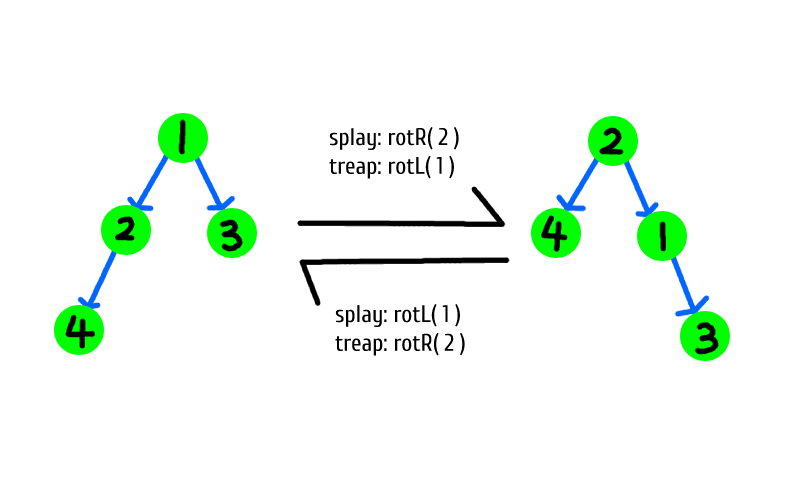
并且,我们还发现,使用0表示左儿子,1表示右儿子的写法,可以同时将左旋和右旋合并在一起,如下:1
2
3
4
5
6
7
8
9
10
11
12
13inline void get(int x) {
return x == ch[fa[x]][1];
}
void rotate(int x) {
int y = fa[x], z = fa[y], k = get(x);
ch[y][k] = ch[x][k^1];
fa[ch[x][k^1]] = y;
ch[x][k^1] = y;
fa[y] = x;
fa[x] = z;
if (z) ch[z][y == ch[z][1]] = x;
up(y);up(x);
}
splay operation
splay操作是伸展树的核心部分,也是比较难的部分。splay本身的目的就是把某一个节点旋转到根节点。在伸展时,需要分情况考虑:
首先,第一种类型是当前节点的父亲就是根节点,那么只需要直接旋转到根节点即可。
第二种类型是当前节点是父亲的左(右)儿子,并且父亲是爷爷的左(右)儿子,那么这个时候需要先让父亲进行旋转,之后再旋转当前节点。
第三种类型是当前节点是父亲的左(右)儿子,并且父亲是爷爷的右(左)儿子,那么这个时候当前节点需要旋转两次。
无论是那一种情况,最后的递归边界为当前节点到达了根节点(父亲为空)。如果还是不太理解的话,建议画一下。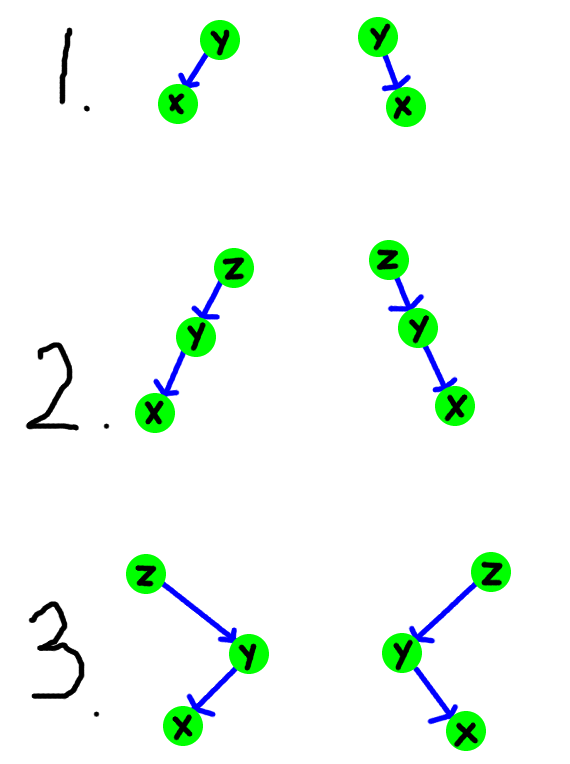
因此,我们可以得到以下的代码:1
2
3
4
5
6
7
8
9
10void splay(int x) {
int f = fa[x];
while (f) {
if (fa[f]) rotate(get(x) == get(f) ? f : x);
rotate(x);
f = fa[x];
}
// 注意要把根节点换了
rt = x;
}
事实上,如果我们把0想象成根节点的父亲的话,我们发现,这个操作事实上就是把某个节点旋转到0的儿子。这样的话,我们可以对这个函数进行一点点简单的修改,使splay操作不仅可以把某一个点旋转到根节点,还可以旋转到某个特定节点的儿子。1
2
3
4
5
6
7
8
9
10// 这个时候k就是我们想要旋转到的某个节点,想旋转到根节点时,调用splay(x,0)即可
void splay(int x, int k) {
int f = fa[x];
while (f != k) {
if (fa[f] != k) rotate(get(x) == get(f) ? f : x);
rotate(x);
f = fa[x];
}
if (!k) rt = x;
}
insert & remove
splay的插入操作遵循BST的规则,即如果要插入的值小于当前节点,则向左儿子走,如果大于当前节点,则向右儿子走,如果相等,并且是可重复的话,当前节点的累计数量+1。伪代码如下:
1 | int rt, tot; // rt为根节点对应的编号, tot表示当前使用的最大的节点的编号 |
删除操作事实上是很类似的,但是更加复杂一点。在删除之前,首先我们要把要删除的节点使用splay操作移动到根节点,如果是给一个值v,然后删除的话,我们需要先得到值v对应的节点的编号x,然后调用splay(x)移动到根节点。并且,移动到根节点后,还要分情况考虑:
如果x没有儿子,直接删除即可。
如果x有一个儿子,则将当前节点删除,并把唯一的儿子作为根节点。
如果x有两个儿子,则需要获取当前节点的前驱(比当前节点小的值当中最大的那个)。然后将该前驱用splay操作移动到根节点,并且直接删除节点x,并将x的右子树作为根节点的右子树即可。(这里可以这样做的原因是这个时候x的左子树必定为空,这是BST的性质)
并且,还要注意删除的时候记得更新节点,并且需要的话根节点也应该更改。
伪代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23void remove(int x) {
remove_to_root(x);
// 节点覆盖次数大于1时,直接减去
if (cnt[rt] > 1) {
cnt[rt]--;
sz[rt]--;
return;
}
if (!ch[rt][0] && !ch[rt][1])
delete(rt);
else if (!ch[rt][0])
delete_leftson(rt);
else if (!ch[rt][1])
delete_rightson(rt);
else {
int p = pre(), cur = rt;
splay(p);
fa[ch[cur][1]] = p;
ch[p][1] = ch[cur][1];
clear(cur);
up(rt);
}
}
maintain an interval
同样的,由于splay的特性,它也很适合被用来维护某一个区间。注意到这个时候,splay中节点的组织形式应该是依据下标的!因此,这个时候splay不一定满足每个节点的val比左儿子大,比右儿子小,它满足的是每个节点的左儿子在数组中的下标一定比该节点小,而右儿子对应的下标一定比该节点的大。这里的想法其实和无旋treap某种程度上是一致的。这里以文艺平衡树为例子简单提一下区间的处理方法。
题目的大意如下:
给一个包含n个数的区间,以及m个操作,每一个操作包含两个整数l,r。要求将区间[l,r]翻转过来。输出最后区间上每个数的值
题目就只有一个区间操作,即翻转。这里,我们同样可以借用之前线段树lazy_tag的思想。当前区间需要翻转时,我们为该节点打上一个标记,并且交换左右儿子即可。当遇到翻转标记时,我们就下传即可。这里的另一个问题是,我们要怎样获得需要的区间呢?和线段树一样吗?和之前的无旋treap一样吗?
考虑下前面我们是怎么获得一段区间的。无旋treap采用的是分裂与合并的思想。直接将需要的区间分裂出来,并打上标记即可。而splay并没有分裂操作,但是由于伸展树的特殊性,我们可以采用两次splay操作获得对应的区间。核心代码如下:1
2
3
4
5
6
7
8// 假设操作的区间是[l,r]
int s1 = find(l-1); // 获得数组中第l-1个元素对应在树上的编号
splay(s1, 0); // 将s1旋转到根节点
int s2 = find(r+1); // 获得r+1对应的编号
splay(s2, s1); // 将s2旋转到s1的儿子(这个时候s2必定为s1的右儿子,且s2左儿子为空)
int x = ch[s2][0]; // 得到对应的区间的编号
rev[x] = !rev[x]; // 更新标记
swap(ch[x][0], ch[x][1]); // 交换左右儿子
注意一下边界情况的处理。(其实可以在原先的树中插入两个节点作为左右边界,这样l-1和r+1就不会溢出了。
summary of splay
这里就简单地对splay做一下总结吧。伸展树作为BST的另一个变种,它的特性比较”神奇”,采用splay操作会使得整颗树需要经常地做调整,就像在”伸展”一样。在时间复杂度上,插入,删除等操作均为O(logn)。当然,需要注意的是,这个复杂度是一个均摊复杂度。和treap类似,splay并不能算严格意义上的”平衡”。在某些情况下,它依然会退化成链表,当然,由于splay操作的存在,即使退化了,它也能比较快地调整回来,因此平均下来,最后的复杂度仍然能够做到O(logn)。当然,splay本身写起来并不算很好写(比起treap的话),不过在实际中应用还是挺广泛的。
summary
数据结构大杂烩系列的第三篇文章到这里就告一段落了。在这篇文章中,我们讲了两种平衡树,treap和splay,这两种平衡树各有特点,并且在时间和空间复杂度上还是十分优秀的。另外,本身平衡树这个知识点就比较难,还是强烈建议去做几道题,这样才能真正地掌握平衡树的核心思想。这里还是推荐NOI2005维修数列这道题,难度稍微有点大,但质量很好。网上的题解有很多,不过质量参差不齐。如果需要的话可以到我的github上找,但没打注释
接下来的话,第四篇文章可能打算写一下关于红黑树的内容,敬请期待吧