Data Structure Note(IV) —— Link/Cut Tree

prologue

　　这是数据结构大杂烩系列的第四篇文章。在上一篇文章中，我们一起学习了两种平衡树——Treap和Splay，并简单地提到几道应用问题。在这篇文章中，我们再次换一个方向，学习一下Link/Cut Tree。这同样是一种比较难的数据结构，用于解决动态树问题。

tree chain split

　　在正式介绍LCT之前，我们先来了解一下树链剖分。这是一种常见的树上的算法，用于维护树上的路径信息。通过将树划分成多条链，并映射到一段连续的数组上，使得我们能够将许多常见的区间维护的数据结构推广到树上(比如线段树)。
　　比如我们可以来看下面的一张图，了解一下树链剖分究竟在做什么事情。(粗的线表示连成了一条链)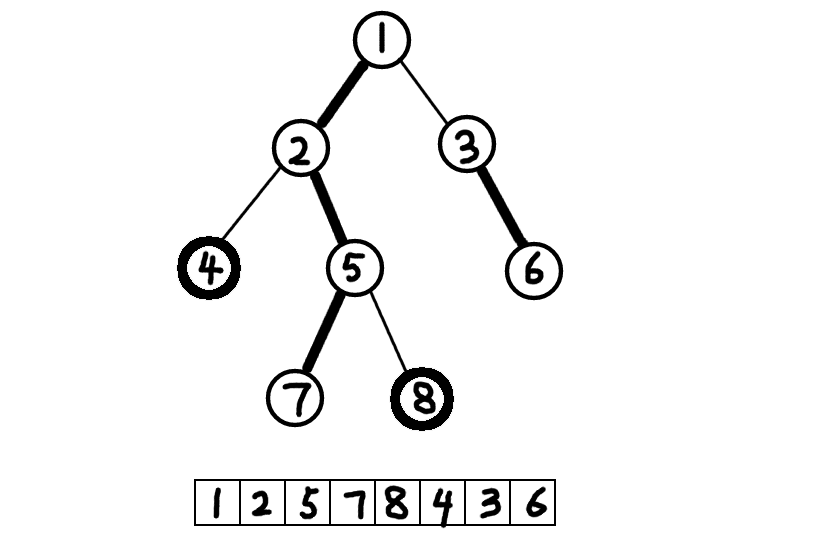
data-structure4
　　从这里，我们可以看到树链剖分的许多特性。整棵树被分成了4条链，分别是1-2-5-7, 3-6, 4, 8。并且，每一个节点属于且仅属于一条链。如果我们把每一条链按照顺序放进一个数组中的话，我们就成功地把一棵树映射到这个数组上了。

how to implement

　　树链剖分问题，简单来说就是轻重链划分的问题。具体来说，我们需要了解以下的概念：

重儿子和轻儿子：对于每一个节点，重儿子为size最大的那个儿子，其余的儿子为轻儿子，如图中，1号节点的重儿子为2，3号为轻儿子。
重边和轻边：与重儿子相连的边为重边，与轻儿子相连的边为轻边。
重链和轻链：由重边连接而成的路径为重链，相反，轻边连成的路径为轻链。

　　我们需要做的，就是将整棵树划分成数条重链。具体的实现操作方法为两次dfs。

// 每个节点的父亲，重儿子，大小，深度
int fa[N], son[N], size[N], dep[N];
// 所在的重链顶端元素，链上的节点编号对应的线段树的编号，线段树对应的编号对应的链上的节点编号
int top[N], tid[N], rnk[N];
// 用链表组织每个点的边
struct edge {
    int to, next;
} e[N<<1];

　　第一次dfs的时候，我们可以得到每一个节点的父亲，重儿子，轻儿子，大小和深度。

void dfs1(int rt) {
    son[rt] = 0;
    size[rt] = 1;
    // 遍历链表
    for (int d = link[rt]; d; d = e[d].next) {
        int to = e[d].to;
        // 没有访问过则访问
        if (!dep[to]) {
            dep[to] = dep[rt] + 1;
            fa[to] = rt;
            dfs1(to);
            size[rt] += size[to];
            // 选择size最大的那个为重儿子
            if (size[to] > size[son[rt]]) son[rt] = to;
        }
    }
}

　　第二次遍历的时候，我们由于知道了每个节点的子树大小，我们可以得到每一条链对应的顶端的节点，并且还可以顺便做从树到线性数组的映射。

void dfs2(int rt, int tp) {
    top[rt] = tp;
    tid[rt] = ++tot;
    rnk[tot] = rt;
    // 没有重儿子，说明没有儿子了，返回
    if (!son[rt]) return;
    // 有重儿子优先遍历，保证最后重链上的元素在线段树中是相邻的！
    dfs2(son[rt], tp);
    // 遍历轻儿子，注意遍历的时候要做判断，防止再次访问到重儿子或者访问到父亲上去
    // 并且，轻儿子的top为它自己
    for (int d = link[rt]; d; d = e[d].next)
    if (e[d].to != son[rt] && e[d].to != fa[rt]) {
        dfs2(e[d].to, e[d].to);
    }
}

　　经过上面的操作后，我们就可以得到一个数组，如前面的图所示。并且，我们可以通过维护这个数组来维护一整棵树的信息。假设这个时候我们使用线段树来维护这个数组，这个时候如果我们要查询8和7的路径上所有点的信息的话，我们可以拆分成[5,7]和[8]，这样，我们就只需要对线段树执行两次查询操作就可以得到答案。由于从根节点到任意节点的链的数量为O(logn)，而线段树区间查询的复杂度为O(logn)，最终我们对于树上路径的信息查询复杂度为O(log²n)，效率还是比较客观的。参考例题：洛谷P3384

link/cut tree

　　好了，在简单了解完树链剖分以后，我们进入正题，看一下LCT究竟是怎样实现的。
　　注意：此处LCT路径是用splay维护的，因此如果还不清楚splay是什么的话，建议先看上一篇文章

a simple problem

　　同样的，我们先来看这样一个问题：

维护一棵树，要求实现以下操作:
修改两点间路径权值，查询两点间路径权值
修改子树权值，查询子树权值和

　　这就是比较明显的树剖模板题了。使用树链剖分将树上的信息映射到数组，并用线段树维护即可。这个时候，如果更改一下条件，我们需要维护的不是一棵树，而是一片森林呢？这个时候就还涉及到树的合并和分离的问题，单纯的树链剖分就不太好做了。
　　这时，我们原先的思路就应该改一下，从而能够顺利解决动态树的问题。其中一种可行的解法就是LCT。

what is LCT

　　LCT是一种用于维护一片森林之间的信息的数据结构，被用来解决动态树问题。它能够实现边的加入和删除，任意两点间的距离信息，连通性，也支持信息的修改等。其中，LCT用到了树链剖分的思想，并且使用splay来进行链的维护。也可以这样理解，LCT实现的是动态的树链剖分。

some basic concept

　　在理解LCT之前，我们需要先来看一些概念。

实链与虚链，类似于树链剖分中的重链和轻链的概念，但实链与虚链是动态的，即可以随时发生更改。每一条实链(包含单个节点)构成了一棵splay树。并且，实链上的所有节点组成的序列是按照深度为关键字进行排序的，即所有splay中节点的左儿子在原先的树中是当前节点的祖先，节点的右儿子在原先的树中是当前节点的儿子！这是很关键的一点。
原树与辅助树。原树即由已知的信息构成的树，辅助树即我们需要去维护的数据结构，一棵辅助树对应一棵原树，一条链对应一个splay，因此，一个辅助树由多个splay组成。参考如下图(实链为实线，虚链为虚线，每一个绿色的区域包围了一个splay)：

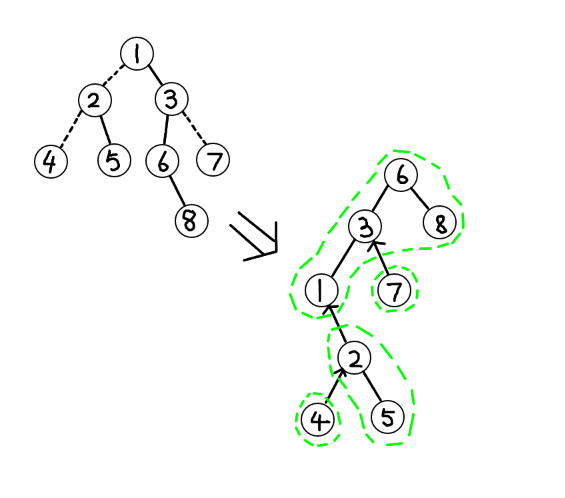
　　通过辅助树，我们能够得到唯一的一棵原树，因此我们只需要维护辅助树即可。而一棵原树往往可以对应于多棵辅助树。并且，在辅助树中，每一棵splay满足中序遍历根节点得到是深度顺序的性质，不同的splay之间单向连接，儿子知道父亲，而父亲并不知道儿子是谁。
　　由辅助树的特点，我们还可以知道，辅助树是可以任意换根的(只要满足性质即可)，并且，在辅助树上能够实现虚链和实链的变换(后面会讲)，这也是我们使用LCT的核心方法。由于LCT需要的方法比较多，下面还是分类别介绍。

variables & basic function

　　LCT需要的变量也比较多，具体如下：

// 每个节点在辅助树中的父亲和儿子，ch[i][0]表示左儿子，ch[i][1]表示右儿子
int fa[N], ch[N][2];
// 每个节点在splay中的子树的大小，每个节点的值，每个节点在splay中的子树的权值和等等
int sz[N], val[N], sum[N] ...
// 翻转标记，用于根的更改操作
bool rev[N];
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
// 判断当前节点是否是父亲的右儿子，用于splay
#define get(x) (x == ch[fa[x]][1])
// 判断当前节点是否是splay中的根节点，注意到根节点和其他splay之间是单向连接的，
// 如果不是根节点，那么必定是其父亲的左儿子或者右儿子。
#define nRoot(x) (ch[fa[x]][0] == x || ch[fa[x]][1] == x)
void up(int x) {
  sz[x] = sz[ls(x)] + sz[rs(x)] + 1;
  sum[x] = sum[ls(x)] + sum[rs(x)] + val[x];
  ...
}
void down(int x) {
  int l = ls(x), r = rs(x);
  if (l) {
    // 标记下传...
  }
  if (r) {
    // 标记下传...
  }
}

splay operation

　　首先，我们需要处理维护splay需要的一些函数。具体和前面splay的写法其实基本上是一样的，除了rotate中需要注意一下和祖先节点的连接，以及splay中需要先将标记下传。

// 旋转操作，和splay类似
void rotate(int x) {
    int y = fa[x], z = fa[y], k = get(x);
    // 注意，此处应该写在前面，否则nRoot判断会出问题
    if (nRoot(y)) ch[z][ch[z][1] == y] = x;
    ch[y][k] = ch[x][k^1];
    fa[ch[x][k^1]] = y;
    ch[x][k^1] = y;
    fa[y] = x;
    fa[x] = z;
    up(y);up(x);
}
// 从上到下更新当前splay树的根节点到x路径上的点
void update(int x) {
    if (nRoot(x)) update(fa[x]);
    if (rev[x]) down(x);
}
// 将当前节点旋转到对应的splay树的根节点
void splay(int x) {
    // 这里由于当前节点的父亲可能具有标记没有下传，应该先将路径上所经过的节点的标记下传，再进行splay
    update(x);
    int f = fa[x];
    while (nRoot(x)) {
        if (nRoot(f)) rotate(get(f) == get(x) ? f : x);
        rotate(x);
        f = fa[x];
    }
}

core method

　　接下来这里就是splay的核心方法了。主要有access和mk_root两个。

access

　　access函数的作用在于，打通当前辅助树中，根节点到某个节点x的路径，即通过虚实链的变换使得节点x与根节点位于同一棵splay中，并且，打通后，在x和根节点所在的splay中，x会成为深度最大的那个节点。且access过后，根节点有可能会发生改变！为了更好的理解access的过程，这里引用一下论文的图片(其中的preferred path在此处即是实链)。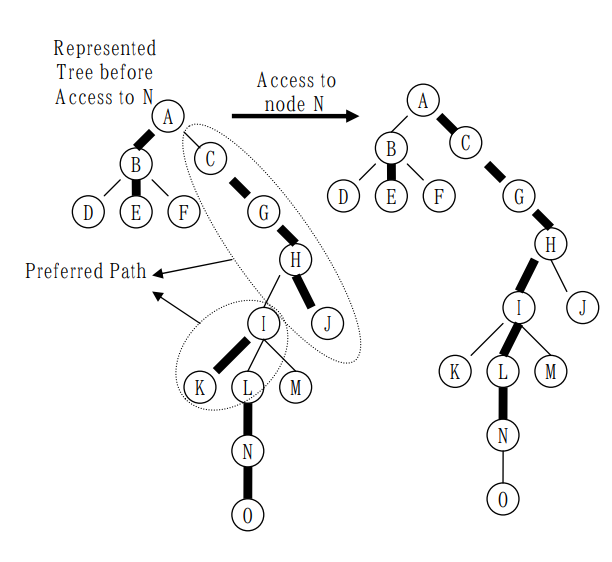
data-structure4
　　考虑一下如果我们要来实现这样的一个过程，那应该怎么处理呢？
　　首先假设最简单的情况，点x和根节点在同一棵splay上面，这个时候我们的处理方式其实就很简单了，只要对x进行splay操作，移动到splay树的根节点，然后单方向地断开x和它的右儿子即可。这个时候满足x是这棵splay的深度最大的点！(右儿子被从这棵树中赶出去了，形成了另外一棵splay树)
　　我们之前的图，调用access(3)后，应该变成了这个样子：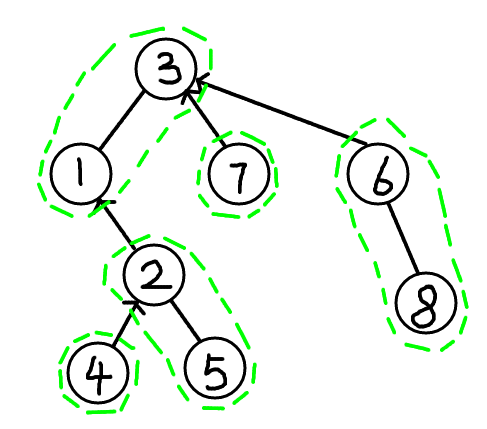
data-structure4
　　其次，我们再来考虑更复杂一点的情况，点x位于splay树A，辅助树的根节点位于splay树B，且树A和B之间直接连接。这个时候就比较麻烦了。但我们还是可以借鉴之前的思路。同样的，我们把点x用splay移动到树A的根节点，并且和右儿子单向断开，分成两棵树C和D，然后，对x的父亲y(由于A和B之间是直接链接的，此时y应该是在树B当中)，我们把它移动到根节点，并且断开右子树，并且，右儿子接到点x上，这个时候，我们就完成了！此时x和根节点在同一棵splay上，且x的深度是最大的。
　　同样的，我们之前的图，调用access(5)后，应该变成了这个样子：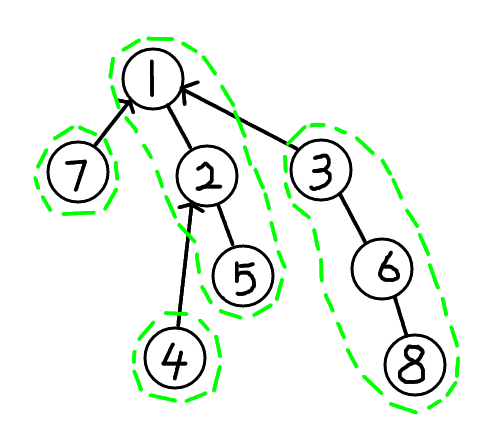
data-structure4
　　那么，如果他们之间不是相邻的呢？其实思路是一样哒!
　　当然，说是很复杂，实际上代码却很短：

void access(int x) {
  for (int p = 0; x; p = x, x = fa[x]) {
    splay(x);
    ch[x][1] = p;
    up(x);
  }
}

　　总的来说，流程大致为：使用splay(x)将当前节点移动到splay树的根节点，并单向断开和右儿子的连接，将右儿子接向上一棵splay树，不断循环，直到到达根节点，此时fa[x]=0，退出。注意到，access事实上是从底向上进行连接的。~~另外，别忘了up操作~~

mk_root

　　理解好之前的access操作后，这个操作也就变得很简单了。make_root(x)，将当前节点变成原树的根节点。这看似很难，实际上只需要用到我们之前的写的几个函数即可。
　　我们考虑一下，如果要让当前节点作为辅助树的根节点的话，那么它有什么特点？它没有父亲！换句话说，它的深度在其所在的树中是最小的。我们有什么好办法可以实现这个呢？
　　前面我们的access操作我们说，access(x)之后，x和根节点位于同一棵splay树中，且x是深度最大的。那么我们如果使用splay操作将x移动到根节点之后，会发生什么？——x的右儿子是空的，节点都在它的左儿子上，这个时候我们如果再使用reverse操作，x的左儿子就空了，这个时候x就变成了splay树中深度最小的那个节点了。换句话说，也就变成了原树的根节点了！另外，别忘了打标记。
　　代码如下：

void mk_root(int x) {
  access(x);
  splay(x);
  rev[x] ^= 1;
  swap(ls(x), rs(x));
}

other function

　　有了之前的那几个操作之后，现在我们几乎可以实现一切了！

find

　　首先是find操作，用于查找节点x所在的原树的根节点。我们只要将原先的根节点和x连通，再把x移动到根节点处，最后不断向左儿子找，就能得到根节点的。思路是很简单的。

int find(int x) {
    access(x);
    splay(x);
    while (ls(x)) {
        if (rev[x]) down(x);
        x = ls(x);
    }
    // 此处splay(x)是为了保证find操作过后，根节点没有发生改变，这句话其实也可以不要
    // 但是后面的link和cut操作就需要做稍微一点点修改
    splay(x);
    return x;
}

link

　　另一个很常见的操作就是link，将两棵树连接到一起。这里要考虑两种情况。
　　第一种是连接的两个点保证合法，那么我们只需要将其中一个点移动到其所在树的根节点，并进行更新操作即可。第二种是两个点不保证合法，那么我们必须确认合法性。什么情况下是不合法的呢？就是两个点本来就已经位于同一棵树中了，这个时候直接连接就破坏了树结构。因此，我们可以直接通过find函数确定x和y是不是在同一棵树上即可。
　　代码也很简单，如下：

void link(int x, int y) {
    mk_root(x);
    // 保证合法，直接连接
    fa[x] = y;
    // 不保证合法的话，需要先做判断
    if (find(y) != x) fa[x] = y;
}

cut

　　有了连接操作，那么必然也会有删除操作，对于两个节点来说，实现删除操作明显比连接操作要复杂一些。先考虑必然合法的情况，我们可以将x使用mk_root移动到根节点，注意到合法性，这个时候x的右儿子必定是y。这个时候只需要双向断开连接即可。
　　接下来考虑不合法的情况，总共有多少种情况呢？首先，第一种情况就是x和y不在同一棵树上，那么我们可以使用find函数判断。第二种情况是x和y在同一棵树上，但是他们没有直接连接，这造成的影响就是，mk_root之后，y的父亲不是x或者y有左儿子！(有左儿子的话说明x和y在原树中不是直接连接的)
　　代码如下：

void cut(int x, int y) {
    mk_root(x);
    // 不保证合法的话，此处需要做一下判断
    if (find(y) != x || fa[y] != x || ch[y][0]) return;
    fa[y] = rs(x) = 0;
    up(x);
}

split

　　接下来，还有一个常见的操作，就是区间的提取。为了方便区间的操作，我们再分离出这样的一个函数，可以把x和y路径上的所有节点提取出来(保证x和y连接)。最后我们可以通过y节点获取整条路径的信息。

void split(int x, int y) {
    mk_root(x);
    access(y);
    // 此处还是需要splay(y) 因为access后x不一定是splay的根了
    splay(y)
}

summary

　　LCT是一种灵活性极强的数据结构，可以实现很多意想不到的功能，当然，它也有一些缺点，比如代码量往往比较大，容易写出bug，还有虽然复杂度是O(log²n)，但是常数比较大等等。但这也不影响它的广泛应用。如果有时间的话，还是可以好好了解一下的。比如做两道题什么的
　　推荐题目:
　　　Sdoi2008Cave
　　　洛谷P3690

epilogue

　　这样，到这里，我们的数据结构大杂烩系列的第四期就结束了，在这篇文章中，我们一开始先简单地提到了树链剖分(很重要的算法，最好要会)，接着，由树链剖分的思想，我们引申到了LCT这种神奇的结构，并且，讲了LCT一些基本的函数和它的思想，最后推荐大家还是去做两道题熟练一下吧。
　　然后之前说好的第四期写红黑树。。网上的介绍太多了，而且我看了下它们讲的好详细啊。所以我想想还是不写了。~~对，没错，我就是鸽子王！~~
　　接下来的话，感觉短时间内可能不会继续更新了，或者换一个话题写了。
　　参考资料：oi-wiki/Link Cut Tree