prologue
这篇博客主要是想探索关于图像压缩方面的算法. 现在流行的图像算法有很多, 像是 jpeg, png, webp 等等. 下面按照类别依次去看下各个算法的实现.
what is Image
了解图片前, 需要知道颜色空间这样的概念. sRGB 是我们常用的一种颜色空间, 在该空间下, 所有的颜色/像素点是由三原色(Red-Green-Blue) 经过混合组成的, 可以用一个三元组表示.
$$(r,g,b) \quad r,g,b \in [0,255]$$
比如 (255,0,0) 表示深红色, (0,255,0) 表示深绿色, (0,0,0) 表示黑色等. 在这样的空间下, 我们一共可以表示 \(2^{24}\) 种颜色, 如果算上透明位, 则可以表示出 \(2^{32}\) 种颜色, 即用 4 个字节表示一个像素. 如果我们有 500 x 500 个像素, 那么我们就可以将其组成一张 500 x 500 的图片. 这是图片最基本的组成.
除此之外, 常用的颜色空间还有 yuv, cmyk 等.
另一个比较有趣的点是, 颜色应该说是一种 “主观” 的判断, 本质上它是一定波长的光. 进入人眼后, 在视网膜上会转化为大脑可理解的信息, 并展示在我们的 “眼前”. 从这个角度上讲, 同一种颜色在不同人看起来长的是不完全一样的(视网膜上感光细胞数量有差异).
gif
gif 是目前一种常用的图片格式, 尤其是在动态图片的领域上应用十分广泛. gif 目前共有两个版本, 分别是 87a 和 89a, 其中 89a 是在原有基础上的一些拓展, 包括定义了应用拓展块等.
gif 在存储图片时, 引入了调色板(palette) 这样一个概念, 每一个索引对应了一个颜色, 存储的数据事实上是一个索引列表. 存储动态图片时, gif 的做法是将每一帧的所有信息都存储下来, 同样是以索引的形式, 然后再定义每一张图片持续播放的时间, 图片连续的切换就形成了动画.
下面是一个基本的 gif 图的组成部分.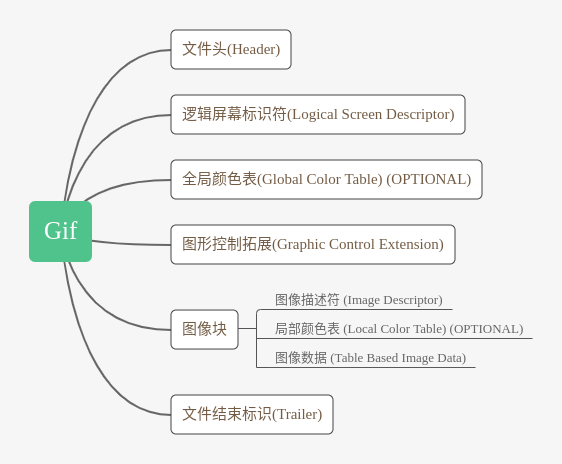
Header
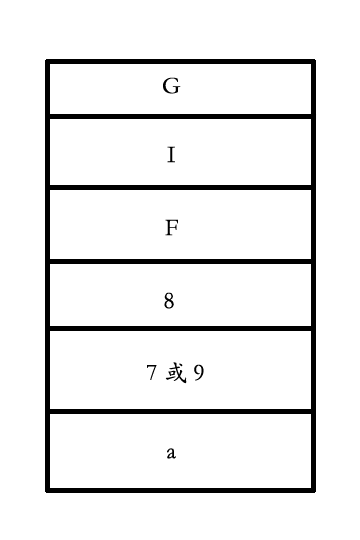
图像头一共六个字节. 包含两个信息, 一个是署名, 即 gif, 另一个是版本号, 包括 87a 或 89a.
Logical Screen Descriptor
逻辑屏幕控制符包括 gif 图的基本信息, 如下图:
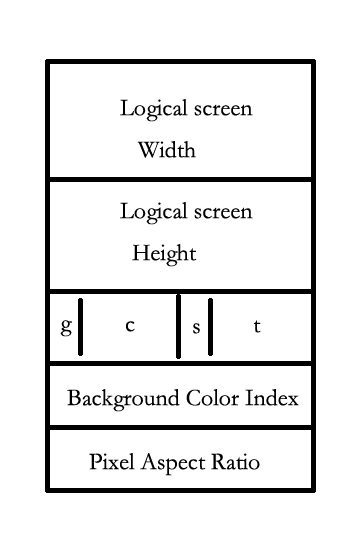
g 表示是否包含全局颜色表, c 用于表示每种颜色的位数(基本用不到), s 表示颜色是否经过排序, \(2^{t+1}\) 表示全局颜色表的大小, 从这里也可以看出, gif 全局颜色表最多只能表示 256 种颜色, 远远小于 RGB 能表示的颜色数量. 最后两个字节则分别表示背景颜色的 index 以及像素长宽比.
Global Color Table
全局颜色表逐个字节按照 r,g,b 的顺序进行排列. 三个字节就表示了一种颜色.

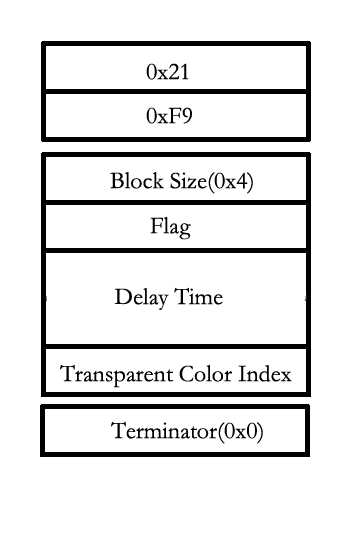
Graphic Control Extension
图像控制拓展是 gif 能够表示动态图片的关键. 前两个字节分别为拓展号(固定为 0x21)以及标示(固定为 0xf9). 接下来分别是块大小(固定为 0x4), 标志位, 延迟时间, 透明色的 index 以及块的终止符(固定为 0). Delay 是重点, 用于描述下一张图片前的间隔, 这样就可以按照一个确定的时间间隔进行图片的展示, 形成 “动画”.
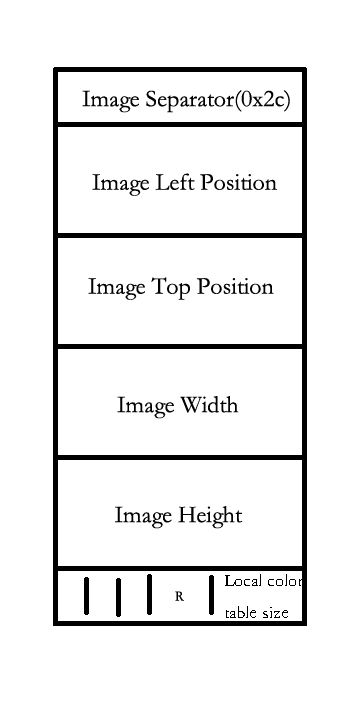
图像块
图像块首先是偏移量(通常为 0)以及宽高(通常为图像大小). 然后就是一些标志位, 记录了是否使用局部颜色表, 透明位等. 接下来则是局部颜色表(如果有的话), 再接着一个初始的 code 位数(用于解压缩), 最后就是一连串的基于表的图像数据了(下称为块). 每个块包含一个 8 位的 size 表示块的大小, 后面则是 size 个字节的用 LZW 算法压缩过的数据. (下图不完全)
Trailer
最后是终止块, 固定值为 0x3b, 表示 gif 文件结束.
LZW Algorithm
lzw 算法是 gif 图像压缩的核心. 在编解码的过程中, 需要动态地维护 code 到一组序列的一一对应关系, 以下以一张用 index 表示的图的编解码为例 (使用 index 在全局颜色表或局部颜色表查找即可获得原始图像).
以下数据来自 gif 的 wiki
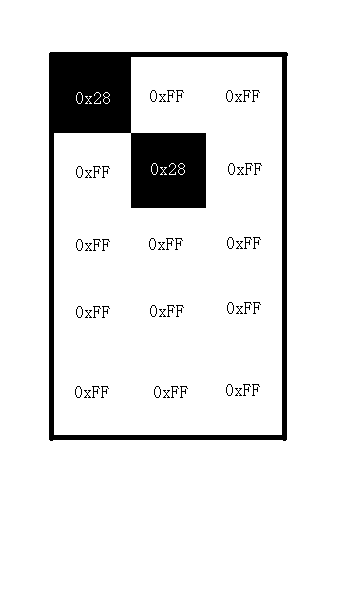
拿到 index 矩阵, 查找全局颜色表, 0x28 对应的颜色为 (0,0,0), 0xff 对应的颜色为 (255,255,255), 则可以得到原图像
Encode
简单起见, 假设仅使用全局颜色表, 并且全局颜色表的 255 中颜色均以填满, 0x28 对应黑色, 0xff 对应白色, 此时, string 到 code 的映射表(下称 table) 中存放了 255 个自映射. 另外, 为了方便控制, 还需要添加两个特殊的映射 clr(0x100) 表示清空后面添加的映射信息, end(0x101) 表示结束. 在这个例子中, 整个编码的过程就是将序列(index)转化为多个 9 位的 code 的过程.
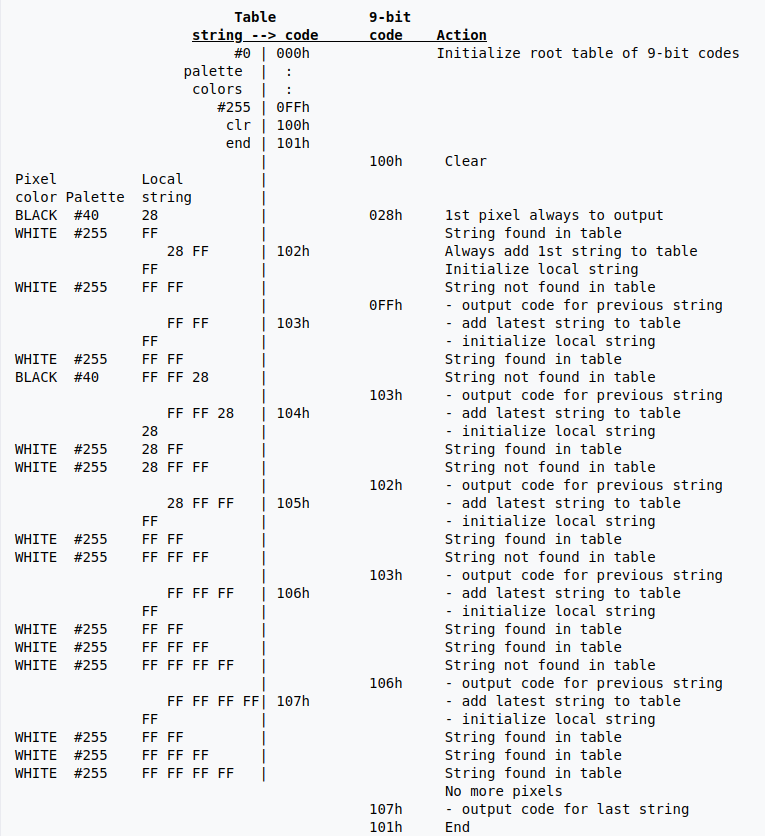
同时, 我们需要维护一个当前最近读入的字节序列(下称 local string, 简记为 ls), 用于生成映射. 按照从左上到右下的顺序, 逐个字节进行读入.
- 输出 clear 对应的映射 0x100
- 读取 0x28, ls = 0x28, 存在于映射表中
- 读取 0xff, ls = 0x28 0xff, 发现当前 ls 不在映射表中, 因此添加映射 0x28 0xff -> 0x102, 同时 ls 只保存最后一位, ls = 0xff, 输出 0x28 对应的映射 0x28
- 读取 0xff, ls = 0xff 0xff, 当前 ls 不在映射表中, 添加映射 0xff 0xff -> 0x103 同时 ls 保存最后一位, ls = 0xff, 输出 0xff 对应的映射 0xff
- 读取 0xff, ls = 0xff 0xff, 存在于映射表中
- 读取 0x28, ls = 0xff 0xff 0x28, 不在映射表中, 添加映射 0xff 0xff 0x28 -> 0x104, ls = 0x28, 输出 0xff 0xff 对应的映射 0x103
- 读取 0xff, ls = 0x28 0xff, 继续
- 读取 0xff, ls = 0x28 0xff 0xff, 添加映射 0x28 0xff 0xff -> 0x105, ls = 0xff, 输出 0x102
- 读取 0xff, ls = 0xff 0xff, 继续
- 读取 0xff, ls = 0xff 0xff 0xff, 添加映射 0xff 0xff 0xff -> 0x106, ls = 0xff, 输出 0x103
- 读取 0xff, ls = 0xff 0xff, 继续
- 读取 0xff, ls = 0xff 0xff 0xff, 继续
- 读取 0xff, ls = 0xff 0xff 0xff 0xff, 添加映射 0xff 0xff 0xff 0xff -> 0x107, ls = 0xff, 输出 0x106
- 读取 0xff, ls = 0xff 0xff, 继续
- 读取 0xff, ls = 0xff 0xff 0xff, 继续
- 读取 0xff, ls = 0xff 0xff 0xff 0xff, 继续
- 没有数据了, 查询 ls 对应的映射 0x107, 输出, 最后输出终止对应的 code 0x101
最后得到序列 0x100, 0x28, 0xff, 0x103, 0x102, 0x103, 0x106, 0x107, 0x101, 将序列展开成 9 位二进制数并紧密排列在一起则得到了图像压缩过后的数据.
Decode
decode 是 encode 的逆过程, 此时, 我们拿到了图像压缩过后的数据, 并且知道每个 code 大小为 9 位, 按 9 位一组展开, 得到 code 序列:
0x100, 0x28, 0xff, 0x103, 0x102, 0x103, 0x106, 0x107, 0x101
由于 decode 是逆过程, 我们需要维护此时应该是 code 到 string 的一一对应关系. 同样我们初始化 255 个自映射以及两个特殊映射.
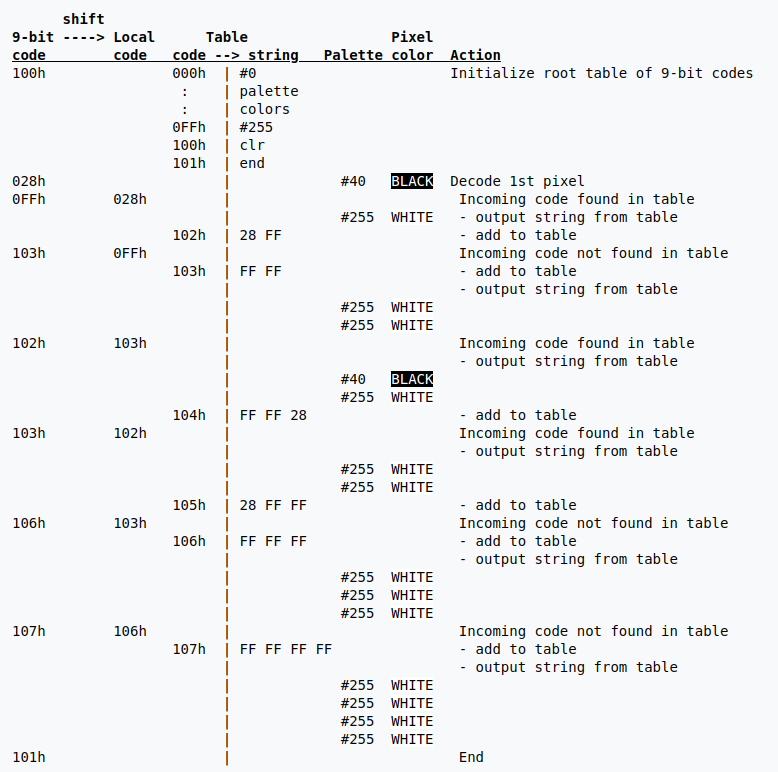
我们用 ls 表示上一个输出对应的序列, 逐个读入 code
如果下一个 code 不在映射表中, 将 ls 和 code 的第一个字节组成的序列放入映射表
如果下一个 code 在映射表中, 将 ls 和 ls 的第一个字节组成的序列放入映射表
- code = 0x100, 初始化
- code = 0x28, ls = 0x28, 输出 0x28
- code = 0xff, 找到映射, 添加映射 0x102 -> 0x28 0xff, 输出 0xff 对应的序列 0xff
- code = 0x103, 找不到映射, 添加映射 0x103 -> 0xff 0xff, 输出 0x103 对应的序列 0xff 0xff
- code = 0x102, 找到映射, 添加映射 0x104 -> 0xff 0xff 0x28(0x103 + 0x102 的第一个 byte), 输出 0x102 对应的序列 0x28 0xff
- code = 0x103, 找到映射, 添加映射 0x105 -> 0x28 0xff 0xff(0x102 + 0x103 的第一个 byte), 输出 0x103 对应的序列 0xff 0xff
- code = 0x106, 找不到映射, 添加映射 0x106 -> 0xff 0xff 0xff, 输出 0x106 对应的映射 0xff 0xff 0xff
- code = 0x107, 找不到映射, 添加映射 0x107 -> 0xff 0xff 0xff 0xff, 输出 0xff 0xff 0xff 0xff
- code = 0x101, 结束解码
最后, 将所有的输出按顺序排序, 得到了原始的 index 序列:
1 | 0x28 0xff 0xff |
再查询全局/局部颜色表即可得到图像的 rgb 信息.
值得一提的是, table 的最大大小为 4096, 但编码器并不一定能保证表填满时会紧接着发送 clear 标志. 在开发过程中, 遇到过网上有些 gif decoder 对于这块的处理默认了编码器在编码的时候会在表满后马上发送 clear, 因此会造成某些 gif 文件无法加载.
png
png(Portable Network Graphics) 是另一种常用的压缩算法. 比较有趣的一点是, png 在刚提出时想要替代 gif 以避免专利问题的.
file format
png 文件更像是一种流式的数据, 本身的组成比较简单. 首先是一个文件头, 包含八个固定字节, 分别为:
1 | 0x89 0x50 0x4E 0x47 |
其中, 第二到第四个字节即为 “PNG” 的 ASCII 形式. 后面几个字节则是各种操作系统的一些用于表示结尾的字符, 包括 CRLF(换行回车) 等.
接下来的则是一连串的固定的 “块”, 每个块的格式是固定的:
| Length | Chunk type | Chunk data | CRC |
|---|---|---|---|
| 4 bytes | 4 bytes | Length bytes | 4 bytes |
其中, type 的四个字节均为区分大小写的 ASCII 字符. 常见的 type 有:
IHDR: 头部块, 包括图片的长宽, 位深, 压缩方式, 图片预处理的方式等, 共 13 个字节.
PLTE: 即 palette, 调色板
IDAT: data 块, 包括使用 IHDR 规定的预处理方式和压缩方式处理过后的图像数据
IEND: 标示块的结束
filter method
filter 是图片预处理的方法. 对于一个图片来说, 通常图片的像素分布越有规律, 图片应该更容易压缩. 比如一张纯色的图片, 可以用类似 (color,offset,length) 这样的三元组对图片进行压缩. 然而, 对于一张渐变的图片, 这样的处理结果却不是很理想. 从直觉上说, 渐变的图片应该是很有规律, 适合压缩的. 这时, filter method 的引入就显得很有必要. 比如我们可以记录 每个点和右(左)边的颜色的差值, 这样处理过后, 我们就可以得到一个所有元素几乎一样的数组矩阵, 这样再去压缩就要容易很多了.
png 的 filter 方法目前总共有 5 中类型:
1 | 0: None 不对图片进行任何处理 |
inflate/deflate algorithm
PNG 内部的图片的数据流采用的是 inflate/deflate 算法进行压缩的, 数据块以 “zlib” 文件格式存储, 至少包含:
压缩方法/标志位: 1 byte
额外的标志/检查位: 1 byte
压缩后的数据: n bytes
检验和: 4 bytes
另外, 根据 RTF1950, zlib 格式还可以包含一个预设的字典, 用于压缩/解压.
png 使用的是无损压缩, 和 zip 的压缩方式基本一致, 基本上原理为: 减小出现频率高的字符的编码长度, 增大出现频率低的字符的编码长度, 即用尽量小的空间去表达原有的信息.
Huffman code
Huffman 编码广泛应用于各种各样的压缩算法中, 其特性可以很好地被用于压缩. 每个叶子节点代表一个需要被编码的字符; 每个节点往左儿子走表示 0, 往右儿子走表示 1, 从根节点到每个叶子节点的路径就变成了一个由 0/1 组成的比特流, 也就是每个字符对应的编码. 比如下面这样一颗 Huffman tree:
1 | /\ Symbol Code |
沿着根节点往叶子节点方向走, 可以得到各个字符对应的编码. 由于只有叶子节点才表示一个待编码字符, 因此所有的编码都不可能是其他编码的前缀. 如果我们有这样一棵树, 给定一个比特序列, 可以唯一地确定一种解码方式, 将比特信息转化为字符, 这样就完成了信息的编解码.
那么, 这样一颗树, 或者说映射关系, 应该如何传输/存储?
在考虑这一点之前需要先思考, 这样的一棵树, 是唯一的吗? 如果我们把上面树中的 C 和 D 对应的 Code 交换一下, 相当于交换了两个左右儿子, 对于编码的长度是没有影响的. 也就是说, 我们更在意的事实上是编码每一个字符所用的比特数, 而不是其具体数值. 因此, 我们可以人为地规定一种树的形状, 只要编/解码器都遵循同一个规范, 最后就可以正常地还原出这样的一棵树出来(比如强制要求每个节点右子树的深度不小于左子树).
在这种情况下, 给定每个字符编码用的比特数, 就可以还原出所有映射关系. 比如上面那棵树, 我们只需要传输 (2,1,3,3) 这样的信息. 算法如下:
1 | 1) 对所有编码长度范围内的所有 i, 统计编码长度为 i 的字符的个数, 存放在 bl_count[i] 中. |
RFC1951 中还给了这样的一个例子, 对于待编码的 8 个字符 ABCDEFGH, 解码器拿到的长度序列为: (3,3,3,3,3,2,4,4), 则按照上面算法的三个步骤的, 可以得到:
1 | step 1: |
LZ77 algorithm
上面解决了编解码的一些问题, 然而还有更重要的问题没有解决, 就是压缩是如何实现的? 还是考虑下面的一张 3x5 的纯白色的图片(每个像素点用三个字节分别表示 RGB 通道):
1 | 0x000000 0x000000 0x000000 |
如果直接传输原始数据, 总共占用了 3x5x3 = 45 个字节, 但这样做总觉得不是很恰当. 其实我们可以考虑, 对于这样一张图片, 我们的大脑是如何去记忆的, 会去记忆每个像素点的值吗? 我想, 大脑记的应该是: “这是一张纯白色的图片, 有 RGB 三个通道, 每个通道有 8 位, 图片大小为 3x5” 这样子. 从这个角度考虑的话, 事实上我们可以用 (15, 0x000000) 这样的二元组去表示, 明显需要传输的信息少了很多. 这样就是一种 “重复利用” 的思想.
对于重复出现的数据, 我们可以用一个 (length, distance) 这样的一个二元组表示这个信息, 说明当前位置和 distance 个比特前的信息是一样的, 且重复了 length 这样的长度, 这样就能较好地利用已有信息. 不过这样又带来了另外的几个问题.
第一个问题是, distance 的长度应该是多少呢? 如果可以为无限大, 这样代价显然有点高, 尤其是对于大文件来说, 编码器可能会不堪重负. 另外, 再考虑到局部性原理, 通常重复的信息出现在当前位置附近的概率较大. 在 zip 以及 png 的默认压缩算法中, 采用的 distance 最大值是 32768. 毫无疑问这样会损失一些压缩率, 但带来的性能上的损耗有些过大了. 同样的, length 的长度也应该有限制, 文档中给出的长度最大为 258, 应该也是综合了性能和压缩率的一个考量.
到目前为止, 我们的一个编码器的简单思路其实已经基本出来了. 我们维护一个大小为 32768 的滑动窗口, 每次读取信息时在滑动窗口内找是否有出现的重复序列, 有则输出 (length, distance) 这样的信息, 没有则直接将字符输出, 直到所有数据处理完毕.
到这里还有一个问题没有解决, 就是解码器应该如何区分下一个读取到的 code 是一个普通的字符还是 (length, distance) 这样的元组呢? 比较显然的做法是, 多加一个 flag 位用于区分. 在 deflate 算法中, 将单独的普通字符信息和 length 合并在一个 code 当中. 每次读取到一个 code 时:
- 0 <= code < 256 纯字符信息, 直接输出
- code = 256 标志数据结束
- 256 < code < 285 表示这是一个长度-距离的二元组
这里其实也有一个对 length 的压缩, 考虑到 length 比较短的概率要比 length 比较长的概率大很多, 并且 length 范围为 3~258, 因此, 这里还有压缩的空间. 如下, 比如读取到一个 code = 257, 则说明读取到 length = 3; 读取到 code = 265, 则再读取一个比特 b, b = 1 表示 length = 12, b = 0 则表示 length = 11.
1 | Extra Extra Extra |
读取到 length 后, 说明下一个字符即为 distance. 同样 distance 也可以采用类似的方法进行压缩, 压缩方式如下:
1 | Extra Extra Extra |
到这里为止, 我们可以得到一个完整的解码器算法:
1 | while 读取得到数据 |
另外, 在数据块中, 还可以选择压缩当前块的方法 type. type = 0 表示不进行压缩, type = 2 表示使用上面说到的方法压缩, type = 1 表示采用一种固定的 huffman 树去编码的, 具体细节在 RFC1951 中.
最后再提一下, png 这里使用的算法属于 LZ 系列. 这个算法最早由 Lempel 和 Ziv 提出, gif 使用的 LZW 算法, 以及 zip/png 使用的压缩算法均属于这个系列, 在多数情况下, 均能有较良好的表现. 不过, 由于这是一种无损压缩, 在图片压缩这样的领域, 这样的算法压缩率还是有些不足的.
information entropy
大概看完了 png/zip 使用的压缩算法, 可能会有这样的一个疑问: 为什么数据能够被压缩呢? 要解释这个问题, 应该还是要从信息论的角度出发. 信息论之父香农(Shannon) 提出的信息熵这样一个概念就能很好地解决这个问题.
考虑一个随机事件 X, 当 p(X) 越小时, 说明该事件出现的概率更小, 则如果出现该事件时, 说明它带来的信息 I(X) 更大. 另外, 由概率论知识, 考虑两个不相关的随机事件 X 和 Y, 有 P(X,Y) = P(X) * P(Y). 同时, 信息量应该具有叠加性, 两个不相关事件带来的信息量之间应该可以相加, 因此得到 I(X,Y) = I(X) + I(Y).
根据以上几个性质, 可以得到信息量的基本公式:
$$
I(X) = -log(p_x)
$$
取遍当前事件空间下的事件集合, 得到信息熵(信息量的期望)为:
$$
H(X) = E(I(X)) = -\Sigma_{i=1}^{n}p_i log_b p_i
$$
其中, 常取 b = 2. 利用这个公式, 我们可以计算出在某个特定分布下数据的信息熵. 比如一个仅由 a,b,c,d 四个字母组成的文本, 给定四个字母出现的概率 p(a)=0.5, p(b)=0.2, p(c)=0.2, p(d)=0.1, 可以得到该分布下, 信息熵为:
$$
H = -(0.5 \cdot log_2 0.5 + 0.2 \cdot log_2 0.2 + 0.2 \cdot log_2 0.2 + 0.1 \cdot log_2 0.1) = 1.2
$$
这个数字告诉我们, 每个字母带来的信息量是 1.2 个比特. 如果我们使用两个比特对数据进行编码, 则对于每个字母, 我们多花了一些比特描述了较少的信息, 这就给数据压缩带来了空间. 使用 huffman 编码, 令 a = 0, b=10, c=110, d=111, 用这样的编码方式可以得到我们编码每个字母使用的比特数的期望为
$$
E = 1 \cdot 0.5 + 2 \cdot 0.2 + 3 \cdot 0.2 + 3 \cdot 0.1 = 1.8
$$
和之前相比, 我们可以使用更少的信息去表达和之前完全一样的信息, 这就是信息的压缩. 而信息熵则给出了无损压缩情形下数据压缩程度的下界(在上面例子下界即为 1.2/2.0 = 0.6). 需要注意的是, 信息熵是基于分布的, 如果数据是完全随机的, 那么采用无损压缩的方式是不可能对数据进行压缩的. 这也告诉了我们, 之所以能对数据进行压缩, 正是因为数据并不是完全无规律的, 比如英文文本中, 一个字节出现的最多的是 0x61~0x7a(A~Z) 以及 0x41~0x5a(a~z), 因此我们可以使用尽量少的比特数去表示这些字节, 使用多一点的比特数去表示那些用得较少的 ascii 码.
jpeg
考虑一个大小为 (1920,1080) 的图片, 假设每个像素包含 RGB 三个通道, 则图片占用的大小为 1920 1080 3 ≈ 6M. 使用 png 的话, 即使有 3:1 的压缩率, 最后的大小也要 2M, 这样的代价有些大了. 因此, 图片更经常采用的是压缩率更高的算法, jpeg.
到 jpeg 这里, 压缩方式则完全不一样了. 之前的几种压缩方式都是属于无损压缩, 而 jpeg 是一种有损压缩的数据格式, 使用 jpeg 压缩过后的数据无法对原有数据完全地还原. 和普通的文件不同, 对于图片来说, 丢失一定的精度的话, 图片还是可以正常浏览, 使用一定精度换取大量的存储空间还是值得的.
color space transformation
考虑这样一个事实: 人的视网膜上的感光细胞中, 主要负责感受光强的细胞数量要远远多于感受光的颜色的细胞数量, 换句话说, 人眼对于光的强弱更加敏感. 因此, 使用 YCbCr 颜色空间要比 RGB 颜色空间要好得多 - 可以方便地分别处理光强和颜色分量. 因此, 编码器在第一步通常会将图片转换到 YCbCr 空间. 具体来说, 则是乘上一个系数矩阵.
$$
\begin{bmatrix}
Y’ \\
C_b \\
C_r \\
\end{bmatrix} =
\begin{bmatrix}
K_R & K_G & K_B \\
-\frac{1}{2} \cdot \frac{K_R}{1-K_B} & -\frac{1}{2} \cdot \frac{K_G}{1-K_B} & \frac{1}{2} \\
\frac{1}{2} & -\frac{1}{2} \cdot \frac{K_G}{1-K_R} & -\frac{1}{2} \cdot \frac{K_B}{1-K_R}
\end{bmatrix}
\enspace
\begin{bmatrix}
R’ \\
G’ \\
B’ \\
\end{bmatrix}
$$
其中, 系数 K 满足 \(K_R + K_G + K_B = 1\), 一种常用的取值为 \(K_R = 0.299, K_G = 0.587, K_B = 0.114\), 这样取值的一个重要理由是: 人眼对于绿色是最敏感的, 而对于蓝紫色是最不敏感的. 因此这里 Y 分量的大小主要是由绿色分量的强度决定.
此外, 由于得到的 Y Cb Cr 三个矩阵大小是一致的, 而 Cb Cr 分量通常不需要那么多, 因此这里可以进行一个采样操作, 将 Cb 和 Cr 矩阵长宽缩减为原来的一半. 不过, 这一步不是必需的.
做完这个预处理后, 下一步就是进行分块的操作了. 目的是减小下一个步骤的计算量. jpeg 会将矩阵切成一个个大小为 8x8 的块, 然后将各个块分别扔到下一步进行处理.
discrete cosine transform
再接着的一个步骤, 也是 jpeg 能做到压缩的一个重要步骤, 就是将图像数据转化到频域空间上去. 这种转化的一个经典做法就是离散傅里叶变换. 不过, 在图像上, 更经常采用的是它的一种特殊形式: 离散余弦变换. 考虑一维的情况, 将八个数据点延拓到负半轴, 同时向右位移半个单位, 则可以得到一个实偶函数(实数并且是偶函数). 傅里叶展开后, 虚数项就可以直接抹去, 最后就得到了离散余弦变换的基本格式:
$$
F_{u} = \frac {1}{c} \Sigma_{x=0}^7 f(x) cos(\frac{(2x+1)u\pi}{16})
$$
将其拓展到二维上, 则可以得到二维的 DCT 变换:
$$
G_{u,v}={\frac {1}{4}}\alpha (u)\alpha (v) \Sigma_{x=0}^{7} \Sigma_{y=0}^{7} g_{x,y}\cos [\frac {(2x+1)u\pi }{16}] \cos [\frac {(2y+1)v\pi }{16}]
$$
其中 \( if \enspace u = 0, \alpha(u) = \frac {1}{\sqrt {2}} \quad else \enspace \alpha(u) = 1\), g 是原矩阵各个元素的值, G 是新的矩阵各个元素的值.
使用这个变换, 我们就可以将原先的图像数据转化到一个频域矩阵. 越靠近左上角表示频率越低的分量, 通常这些低频分量会比较大, 越靠近右上角表示频率越高的分量, 这些高频分量通常比较小, 用于展示图像的细节, 高频分量对于图像来说往往不是那么重要, 如果能舍去高频分量, 那么我们就可以保留低频数据, 实现对图像的压缩.
quantization
上一步中得到了频率数据后, 接下来的一个步骤则是去掉高频信息. 然而, 要去掉多大范围的高频信息呢? 为了在尽量保证压缩率的同时避免过多的细节丢失, jpeg specification 中给出了这样一个量化矩阵去进行去高频的操作:
$$
Q={\begin{bmatrix}
16&11&10&16&24&40&51&61 \\
12&12&14&19&26&58&60&55 \\
14&13&16&24&40&57&69&56 \\
14&17&22&29&51&87&80&62 \\
18&22&37&56&68&109&103&77 \\
24&35&55&64&81&104&113&92 \\
49&64&78&87&103&121&120&101 \\
72&92&95&98&112&100&103&99 \\
\end{bmatrix}}
$$
将频域矩阵所有元素除以量化矩阵, 然后再向下取整, 就可以得到经过量化操作后的信息, 即对原有矩阵进行一个这样的操作:
$$
B_{j,k}= round(\frac {G_{j,k}}{Q_{j,k}}) \quad j \in (0,7); k \in (0,7)
$$
可以看到, 量化矩阵 Q 中, 靠近右下角的信息需要除以一个更大的数字, 最终我们可以得到一个系数矩阵 B, 并且 B 中右下角存在大量的 0(大部分高频信息被抹去了), 同时也保证了高频信息的系数较大时, 仍然有一定的保留.
entropy encoding
拿到量化过后的矩阵后, 最后一步就是编码了. 考虑到左上角到右下角的数据基本是单调递减的, 对于这样的数据, 一个比较好的处理方式就是按照 zig-zag 的方式将其转为数组. 对于每个块, 按照下面的顺序排列成一位数组:
(图来自 wiki)
最坐上角的元素决定了整个块的色调, 因此被称为 “直流系数”(DC coefficient). 其余的 63 个数字被称为 “交流系数”(AC coefficient). 对于每个块中的 DC coefficient, 其值通常比较大, 采用的是记录每个块的系数的差的方式. 而 AC coefficient 采用的是行程编码(“run-length encoding”).
按照下面的格式进行:
| Symbol1 | Symbol2 |
|---|---|
| (length, size) | (data) |
length 表示当前位置到上一个非 0 AC 系数中间的 0 的数量, size 表示当前位置的值要用几个位的数字来表示(注意这里不是 data 对应的二进制数字有多少位, 因为 data = 0 不需要编码, size = 0 即可表示, 具体 data 对应的位数可以查表得到), 并且, length 和 size 各占四个 bit, 合起来占据一个字节. data 即为 size 位二进制数, 比如下面这段数字:
1 | 5, 16, 0, 0, 2, 0, 3, 0, 0, 0, 1 |
经过编码后, 则变成:
1 | (0,3)(5) (0,5)(16) (2,1)(2) (1,1)(3) (3,1)(1) |
最后, 再将这些数字使用 huffman 编码转成一个比特流(序列化), 就完成了整个 jpeg 的压缩流程了.
epilogue
这篇文章到这里就结束了. 整个文章中, 简单地浏览过了 gif, png, jpeg 的编码方式, 了解了如何对一个图片进行压缩, 后面有时间的话可能再学习一下音视频的编码方式吧.