prologue
这是数据结构大杂烩系列的第二篇文章。在前一篇文章中,我们学习了线段树及一些相关的数据结构。我们简单地了解了线段树是如何构造,如何维护的,并简单地了解了它的应用。今天,就让我们一起再深入学习它吧。
今天的主题是可持久化线段树,这是一种能存储区间“历史变化”的数据结构,本身代码量不大,但理解起来还是有一定难度的。
注:本文假设读者对线段树已经有了一定的了解。如果不知道线段树是什么,请先前往Data Structure Note(I)
a simple problem
国际惯例,在深入学习相关概念之前,我们先来了解一下这样一种问题。我们知道,线段树能维护区间的最大值最小值,可如果我们要的是区间的第K大值呢?
给定一个数组n,然后有m个询问,每个询问包含三个值L,R,K,要求输出在[L,R]区间上的第K大值(K <= R - L + 1)
同样的,最直接的做法就是直接扫描区间[L,R],拿出所有元素并从大到小排序,最后输出第K个值即可。当然,很明显这样的做法是不可取的——复杂度高达O(mnlogn),我们发现,在这样一种情况下,我们对元素进行排序实际上做了很多“无用”的操作,我们仅仅需要第K大的值,但排序却得到了所有数字的大小顺序,显然有些冗余。那么有没有什么好的办法呢?有的,就是可持久化线段树(下称主席树)
before we learn
weighted segment tree
在正式进入主席树之前,我们需要先理解好权值线段树这一概念。本身权值线段树也是一种线段树,和我们在上一篇文章中提到的线段树的主要区别在于,权值线段树中叶子节点的概念不太一样。比如下面的一个数组a[]=[3,2,1,5,5,7,8]。按照之前的线段树的概念,这个时候线段树是根据下标建立的。因此,线段树一共有七个叶子节点,其中每个节点的值分别为3,2,1,5,5,7,8
那么对于权值线段树呢?由于这是按照值建立的树,通常情况下,这颗树应该有八个叶子节点(数组a中的数字的值域为[1,8])。并且,每个叶子节点中的值表示的应该是某个权值出现的次数。如果还不太理解的话可以看下图。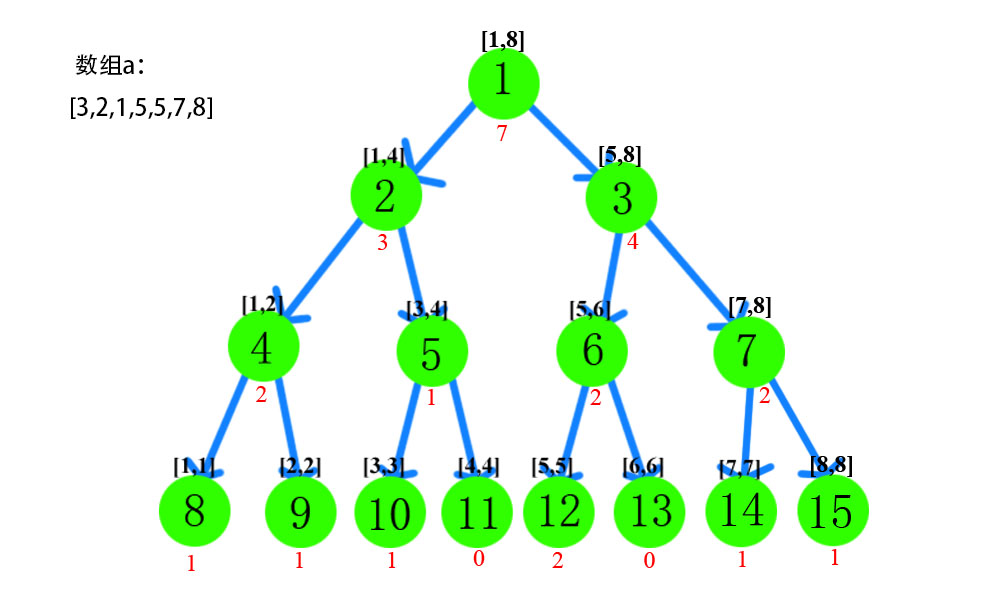
为什么要提到权值线段树呢?答案还是在图中。结合之前我们学习的关于线段树相关的知识。我们发现,权值线段树天生就可以被用来查找区间的第K大值,并且还是在logn的复杂度下。下面为伪代码:1
2
3
4
5
6
7void search(int rt, int l, int r, int k) {
if (l == r) return l
// 当左儿子的权值w<=k时,说明左儿子至少有k个数,第k大的一定在左儿子
// 否则第k大的数一定在右儿子,且是右儿子中第k-w大的数
if (左儿子权值不大于k) search(lson(rt), l, mid, k)
else search(rson(rt), mid+1, r, k - weight(lson(rt)))
}
这样,我们就发现,如果对整个数组建立一颗权值线段树的话,我们可以在logn复杂度的前提下,得到整个数组中第k大的数字,我们成功地向答案迈进了第一步!
再考虑一下,如果我们只是对部分数组建立权值线段树呢?比如,将区间[1,x]的所有数字放在一起,建立一颗权值线段树,按照上面的逻辑,我们就可以获得区间[1,x]中任意第k大的数字了。
再前进一步,如果我们能够对区间[l,r]建立一颗权值线段树,那么我们是不是就可以得到区间的第k大的数字了呢?恩,这个就是主席树基本原理之一。
weighted segment tree’s operations
前面我们说,如果能对所有的区间建立线段树的话,我们就可以顺利地解决区间的第k大问题了,但是这样的复杂度未免也太高了。区间总数为O(n^2),建树的复杂度是O(nlogn),合起来的复杂度高达O(n^3 logn),当然,即使时间上能接受,空间上也接受不了。因此,我们必须想办法减少开销。一个可行的办法是,利用权值线段树可以做减法的特点。这是什么意思呢?比如我们现在得到了在区间[1,x]和区间[1,y]上建立的两颗权值线段树(y>x),这个时候这两颗树之间所有对应的节点之间做减法,我们就可以得到在区间[x+1,y]上建立的权值线段树。如果不能理解,可以参考下图。(这里建议自己画图理解理解,这是解决主席树问题的关键一步)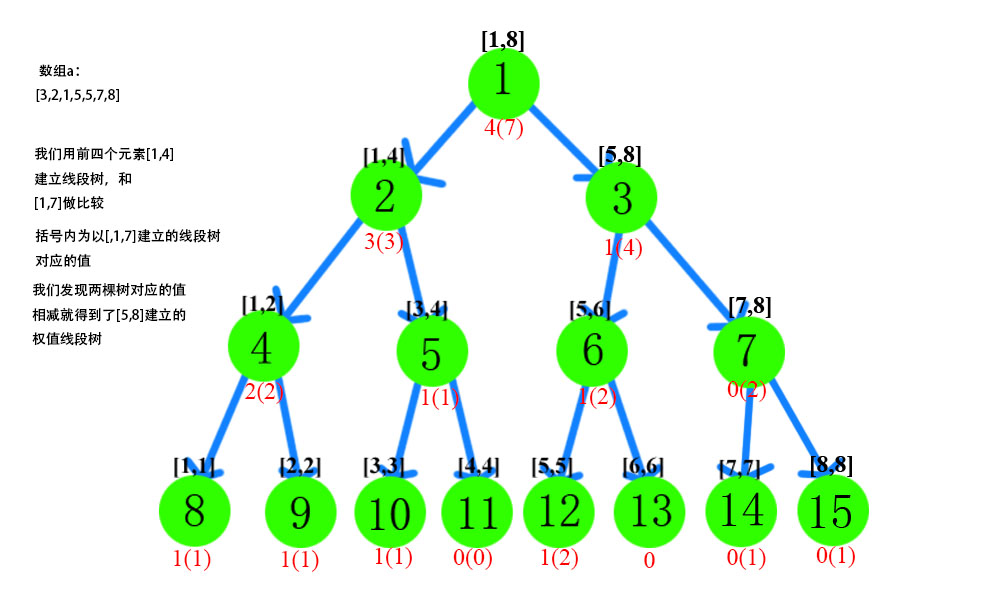
make full use of last tree
前面我们得到了这样一个结论:两颗权值线段树[1,x],[1,y]之间做减法,可以直接得到第三颗权值线段树[x+1,y]。因此,我们只需要建立O(n)颗线段树就好了。这样,我们就再次降低了复杂度。但是,我们又发现了另一个问题,对于以区间[1,x]和[1,x+1]建立的两颗线段树来说,其实发生变化的最多只有logn个节点(想想为什么),因此,它们之前很多信息是重复的,如果我们能够重复利用这段信息的话,那样也许就能降低复杂度了。
如果要利用前一颗线段树的信息,最直接的办法就是直接复用前一颗线段树的节点,对于当前的节点,如果左儿子的信息需要更新,那么我们就重新开一个点,将当前节点的左儿子连接到新开的点,并赋予新值,将当前节点的右儿子连接到前一颗线段树对应的节点即可。
这个思想很简单,但却是主席树的精华所在。同样的,如果不是很理解,可以参考下图。当然,这里还是同样建议自己试着画图,更有助于理解。
persistent segment tree
现在,我们终于可以正式进入主席树了。其实,大部分要讲的东西已经讲完了。这里还是贴一下代码吧,结合代码理解起来会更方便一些。这里以POJ2104为例子,简单地提一下主席树的写法。
build
在建树的时候,要注意一个问题,对主席树而言,建树的空间复杂度为O(nlogn),因此,建议在申请空间时,直接开一个(N<<5)大小的数组,避免空间不够导致的错误。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int a[N], b[N]; // a, b数组用于读入数据,与题目有关
int tot = 0; // 动态开点,注意,不建议使用malloc,效率过低
int rt[N], lson[MAXN], rson[MAXN], sum[MAXN];
// rt[i]表示建立的第i颗树的树根index
// lson[i]和rson[i]分别表示index为i的节点的左右儿子的index,注意到不能用i<<1和i<<1|1表示左右儿子了
// sum[i] 表示当前节点所对应的区间的值的出现次数
// main函数中使用build(rt[0], 1, n)进行建树即可
void build(int& x, int l, int r) {
x = ++tot;
sum[x] = 0;
if (l == r) return;
int mid = mid(l,r);
build(lson[x], l, mid);
build(rson[x], mid+1, r);
}
update
更新的操作其实和线段树基本一样。但每一个节点都是动态开启的。记得将当前树和上一颗树关联起来即可。1
2
3
4
5
6
7
8
9
10
11
12
13// 具体建树的时候,扫描一整个数组,对于每一个值(注意不是下标),
// 调用update(rt[x], rt[x-1], 1, n, a[x])即可
void update(int& x, int lrt, int l, int r, int pos) {
x = ++tot;
sum[x] = sum[lrt] + 1;
if (l == r) return;
lson[x] = lson[lrt]; // 此处将当前节点与上一颗树的左儿子连接在一起
rson[x] = rson[lrt]; // 右儿子同样
int mid = mid(l,r);
// 如果需要更新的在左儿子,将左儿子传入,注意到lson[x]的值在下一层迭代中会被覆盖,即开启了新的节点,右儿子同理
if (pos <= mid) update(lson[x], lson[lrt], l, mid, pos);
else update(rson[x], rson[lrt], mid+1, r, pos);
}
query
1 | // 查询区间[L,R]时,调用query(rt[R],rt[L-1],1,n,k)即可 |
something else
在处理实际问题的时候,我们还需要注意一个问题。建立权值线段树的时候,通常权值的范围可能在-2^31~2^31-1之间,对于这样大的一个范围,显然我们是不可能建立线段树的,因此比较合理的做法应该是使用在上一篇文章中提到的离散化,将权值映射到区间[1,n]上,并进行去重操作,这样复杂度就变得很合理了。在C++中,可以这样写:1
2sort(b+1, b+n+1);
int m = unique(b+1, b+n+1) - (b+1);
其中,sort用于对数组进行排序,unique用于去重,返回的是尾指针。
另外,如果理解了主席树的思想的话,我们会发现,一开始我们使用build函数的时候,建立的树rt[0]事实上是空的,因此build函数是可以不用的,直接for循环并且动态地添加每一个点即可。
总的来说,主席树在建立新的树的时候,用的是动态开点,每一次更新操作,时间和空间复杂度均为O(logn)。建树总时间和空间复杂度均为O(nlogn),对于询问的总复杂度为O(mlogn),这样就都降低到可以接受的范围内了。并且,主席树最核心的思想在于它充分利用了前一颗树的信息,大幅度降低了复杂度。现在,我们能够成功地解决在文章一开始的时候提出的问题了。(建议做一道模板题以加深理解。
level up - count on a tree
之前,我们利用主席树解决了区间的第k大的问题,现在,我们题目的难度升级了,如果是要求在树上的第k大值呢?恩,还是用主席树,那么这个时候又该怎么处理呢?之前我们能够求出区间上的第k大的值,是因为区间是连续,而且是线性的,我们能够使用sum[R]-sum[L-1]得到区间[L,R]上的值,然而,如果是在一颗树上的话,它并不满足线性这一条件。那该怎么办呢?
一个可行解是对我们的答案进行差分。对于在树上的两个点u和v,他们之间有且仅有一条唯一的路径,这个时候,假设他们的最近公共祖先(lca)为t的话,那么u和v上的点的权值的和变成sum[u]+sum[v]-sum[t]-sum[fa[t]]。这里,fa[t]表示t的父亲节点,注意,这里同样用到了权值线段树可以进行减法的特性。并且,这里的sum[x]表示的应该是当前节点x到根节点的所有值建成的权值线段树。如果能理解好这一点的话,那么这个问题也就变得很简单了。
具体实现时,我们只需要在更新的时候,调用update(rt[x],rt[fa[x]],1,n,a[x]),即使用当前节点的父亲节点去更新当前节点,并且,query需要进行一定的更改,具体如下:
1 | // 调用的时候为query(1,n,u,v,lca(u,v),fa[lca(u,v)],k)即可 |
how to find lca
查询最近公共祖先的方法有很多(不知道这个算不算是数据结构的知识)。其中一种可行的解法就是采用倍增,在O(nlogn)的预处理后,能在O(logn)的复杂度下求得最近公共祖先。另外一种可行的解法是采用树链剖分,也是一种数据结构中的常用算法,这里就不进行赘述了。
level up up!
前面我们处理的都是静态的第k大值的问题,但是实际应用中我们往往会遇到很多动态的情况。比如操作中包含对某些点的更新,在这种情况下区间的第k大值的话,难度就很大了。前面我们处理区间第k大值的时候,是按照从左到右的顺序逐步插入点的,并且建的是权值线段树,这个时候如果我们要更改第x位的数字的话,那么后面rt[x+1]~rt[n]都要进行更改,这样的代价很明显是不可取的。那么我们就必须换一种思路。这里以洛谷P2617为例
给一个长度为n的序列,以及m个操作,包含两种类型,一种是求[l,r]区间上的第k大值,另一种是修改当前数组中某个元素的值。
对这道题来说,我们要实现的是单点修改和区间查询两种操作。要满足修改操作的话,那么我们又必须对后面的所有数,即区间进行更新。那么我们能不能减少更新的数量呢?仅仅更新一部分主席树即可。像上一篇文章中求前缀和的问题一样,用一个sum数组累计前缀和的话,遇上有单点修改操作的时候,sum数组后面所有数字都要进行修改。当时我们用的是线段树和树状数组解决的。那么对于这个问题,是不是可以采用类似的思路呢?
结合这道题而言,我们选择采用了树状数组来实现。(理论上也是可以用线段树实现的,但是线段树的复杂度在常数上略输一筹)。注意到,这个时候,每一颗主席树中每一个点代表的是一段前缀和,并且,在更新的时候,只能用自身的信息来更新自身,否则会破坏树状数组的结构。
并且,由于这道题中有单点修改操作,因此在建树的时候我们必须先进行离线操作,将修改的值也放进数组当中并进行离散化处理。
几个核心函数如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38void update(int pre, int& now, int l, int r, int v, int type) {
now = ++tot;
sum[now] = sum[pre] + type;
if (l == r) return;
lson[now] = lson[pre];
rson[now] = rson[pre];
int mid = mid(l,r);
if (v <= mid) update(lson[pre], lson[now], l, mid, v, type);
else update(rson[pre], rson[now], mid+1, r, v, type);
}
// type为1加上,-1表示减去
// x表示的是在原数组a中的下标,使用lower_bound得到其在离散化后的数组的位置
// 注意到使用树状数组,每次更新点x的时候,还要更新x+lowbit(x)的主席树
inline void add(int x, int type) {
int pos = lower_bound(b+1, b+m+1, a[x]) - b;
while (x <= n) {
update(rt[x], rt[x], 1, m, pos, type);
x += lowbit(x);
}
}
// 同样的,由于使用树状数组,这里需要加上(减去)所有沿着树状数组路径上的主席树
int query(int l, int r, int k) {
if (l == r) return l;
int x = 0;
for (int i = 1; i <= tl; i++) x -= sum[lson[ql[i]]];
for (int i = 1; i <= tr; i++) x += sum[lson[qr[i]]];
int mid = mid(l,r);
if (k <= x) {
for (int i = 1; i <= tl; i++) ql[i] = lson[ql[i]];
for (int i = 1; i <= tr; i++) qr[i] = lson[qr[i]];
return query(l, mid, k);
} else {
for (int i = 1; i <= tl; i++) ql[i] = rson[ql[i]];
for (int i = 1; i <= tr; i++) qr[i] = rson[qr[i]];
return query(mid+1, r, k - x);
}
}
// 如果需要整个题目的代码的话,也可以联系我哈(其实网上好多题解的)
这种写法的话,时间和空间上复杂度均为O(nlog2n),开销是很大的。但貌似没有什么更好的办法了。(如果有还请告诉我)
last but not least
重新回到我们的主题上面来,我们一开始提的问题是,求解一个区间上的第K大值的问题,当然,上面讨论的使用主席树的写法其实主要是用于多次询问,如果只有一次询问的话,很显然我们完全没必要这么麻烦。我们可以直接使用sort,然后输出第k个数即可。我们也可以使用选择排序,第k个选择的数就是第k大。我们甚至可以使用哈希进行计数排序。貌似也可以使用堆排序进行处理。当然,还有一种使用基于快速排序思想的求第k大的算法。
这里想说的其实是,对于一道同样的问题,它的解法有可能是多样化的,并且,对于不同的数据规模,可能也有不同的优秀算法,因此,最好不要拘泥于某一中特定的算法(当然,解法唯一的题目还是有的吧)。
(包括很多看起来很难的题目,由于数据比较水,暴力还是可以拿到很多分的,甚至AC
epilogue
数据结构大杂烩系列的第二篇文章在这里就告一段落了(其实这篇文章严格意义上来说应该算是第一篇文章的补充)。同样的,我们一开始引入一个区间第k大的问题,然后,顺着这个话题,讲到了权值线段树的一些概念,一步一步推出主席树建立的思想过程,接着,再通过一道模板题,简单地提了一下主席树的写法。再接着,我们又将题目难度升级,尝试着求解树上的第k大问题,再后面,我们又提到了带单点修改的主席树的写法(其实严格意义上说这个应该算是树套树)。最后,我们再一次地回到了主题,关于求解区间的第k大的问题。当然,如果要理解清楚的话,还是只能自己去做几道题,这里目的仅仅是提一下主席树的思想而已。
下一篇文章的话可能要比较久后才出来,也有可能写算法相关的一些博客,敬请期待吧。(在做了.jpg